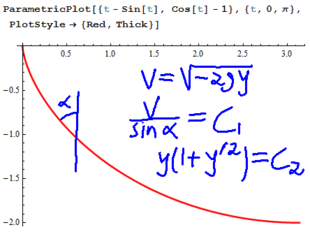12-267/Homework Assignment 3: Difference between revisions
Mathstudent (talk | contribs) No edit summary |
No edit summary |
||
| (3 intermediate revisions by one other user not shown) | |||
| Line 13: | Line 13: | ||
# <math>y\mapsto\int_a^b\frac{y'^2}{x^3}dx</math>. |
# <math>y\mapsto\int_a^b\frac{y'^2}{x^3}dx</math>. |
||
# <math>y\mapsto\int_a^b(y^2+y'^2+2ye^x)dx</math>. |
# <math>y\mapsto\int_a^b(y^2+y'^2+2ye^x)dx</math>. |
||
# <span style="color: red">Postponed!</span> <math>y\mapsto\int_0^1(y'^2+x^2)dx</math> subject to <math>\int_0^1y^2dx=2</math> and <math>y(0)=0</math> and <math>y(1)= |
# <span style="color: red">Postponed!</span> <math>y\mapsto\int_0^1(y'^2+x^2)dx</math> subject to <math>\int_0^1y^2dx=2</math> and <math>y(0)=0</math> and <math>y(1)=0</math>. |
||
'''Task 3.''' A roach <math>R</math> I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying <math>R</math>'s life, help it find the fastest path from one point in the upper half plane <math>\{y>0\}</math> to another point in the upper half plane, assuming there is only one wall around, built along the <math>x</math>-axis <math>y=0</math>. |
'''Task 3.''' A roach <math>R</math> I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying <math>R</math>'s life, help it find the fastest path from one point in the upper half plane <math>\{y>0\}</math> to another point in the upper half plane, assuming there is only one wall around, built along the <math>x</math>-axis <math>y=0</math>. |
||
{{Template:12-267:Dror/Students Divider}} |
|||
[http://drorbn.net/index.php?title=Image:012.jpg Solution to HW3, page 1] [[User:Mathstudent|Mathstudent]] |
|||
[http://drorbn.net/index.php?title=Image:013.jpg Solution to HW3, page 2] [[User:Mathstudent|Mathstudent]] |
|||
'''Solution to Task 1.''' --[[User:Twine|Twine]] 18:11, 24 October 2012 (EDT) |
|||
[http://drorbn.net/index.php?title=Image:014.jpg Solution to HW3, page 3] [[User:Mathstudent|Mathstudent]] |
|||
[http://drorbn.net/index.php?title=Image:015.jpg Solution to HW3, page 4] [[User:Mathstudent|Mathstudent]] |
|||
Let <math>\sum_{n=1}^\infty c_n = S</math>. We have that <math>\lim_{n \rightarrow \infty} c_n = 0</math>. |
|||
Let <math>\epsilon > 0</math>. |
|||
<math>\exists N \in \mathbb{Z}^+</math> such that <math>\sum_{n=1}^N c_n > S - \epsilon</math>. |
|||
Choose such an N. Then <math>\sum_{n=N}^{\infty} c_n < \epsilon</math>. |
|||
Then <math>\forall x \in X, \forall m > N, n>N</math>, we have <math>|\Phi_n(x) - \Phi_m(x)| < \epsilon</math>. |
|||
As this result is independent of our choice of x, we have by the cauchy criterion that <math>\Phi_n</math> is uniformly convergent and <math>\lim_{n \rightarrow \infty} \Phi_n(x) = \Phi(x)</math> exists. |
|||
Solutions to HW3: [[User:Mathstudent|Mathstudent]] |
|||
<gallery> |
|||
Image:012.jpg|page 1 |
|||
Image:013.jpg|page 2 |
|||
Image:014.jpg|page 3 |
|||
Image:015.jpg|page 4 |
|||
</gallery> |
|||
Latest revision as of 08:49, 25 October 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday October 9. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.
Task 0. Identify yourself in the Class Photo!
Task 1. Let be a sequence of functions defined on some set , and suppose that some sequence of non-negative reals is given such that for every , . Suppose also that is finite. Prove that the sequence is uniformly convergent.
Task 2. Find the extrema of the following functionals:
- subject to and .
- subject to and .
- subject to and .
- .
- .
- Postponed! subject to and and .
Task 3. A roach I once met was mortally afraid of walls, and so when it walked on my kitchen's floor, its speed was exactly proportional to its distance from the nearest wall (that is, very near a wall it crawled very slowly, while in the centre of the room it run around quickly and happily). As a step towards simplifying 's life, help it find the fastest path from one point in the upper half plane to another point in the upper half plane, assuming there is only one wall around, built along the -axis .
| Dror's notes above / Student's notes below |
Solution to Task 1. --Twine 18:11, 24 October 2012 (EDT)
Let . We have that .
Let .
such that .
Choose such an N. Then .
Then , we have .
As this result is independent of our choice of x, we have by the cauchy criterion that is uniformly convergent and exists.
Solutions to HW3: Mathstudent