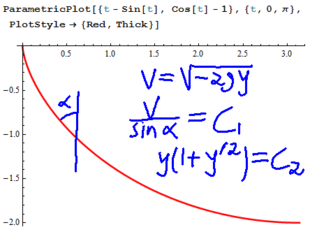|
|
| Line 10: |
Line 10: |
|
# <math>\frac{dy}{dx}=\frac{x-e^{-x}}{y+e^y}</math>. |
|
# <math>\frac{dy}{dx}=\frac{x-e^{-x}}{y+e^y}</math>. |
|
# <math>xdx+ye^{-x}dy=0</math>, with <math>y(0)=1</math>. |
|
# <math>xdx+ye^{-x}dy=0</math>, with <math>y(0)=1</math>. |
|
# <math>\frac{dy}{dx}=\frac{ax+b}{cx+d}</math>, where <math>a,b,c,d</math> are constants. |
|
# <math>\frac{dy}{dx}=\frac{ax+b}{cx+d}</math>, where <math>a,b,c,d</math> are arbitrary constants. |
|
# <math>\frac{dy}{dx}=-\frac{ax+by}{bx+cy}</math>, where <math>a,b,c</math> are constants. |
|
# <math>\frac{dy}{dx}=-\frac{ax+by}{bx+cy}</math>, where <math>a,b,c</math> are arbitrary constants. |
|
# <math>0=(e^x\sin y + 3y)dx - (3x-e^x\sin y)dy</math>. |
|
# <math>0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy</math>. |
Revision as of 14:57, 17 September 2012
| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
 Monday: Separated equations, escape velocities. HW1. Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
 Monday: Solving exact equations, integration factors. HW2. Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo. Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
 Monday: Last notes on the fundamental theorem. HW3. Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange. Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
 Monday: Euler and improved Euler. Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
 Monday: Multiple roots, reduction of order, undetermined coefficients. Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
 Monday: The basic properties of matrix exponentiation. Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples. Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
 Monday: Non-homogeneous systems. Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs. Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math]. Friday: Series solutions for [math]\displaystyle{ y'=f(x,y) }[/math].
|
| 11
|
Nov 19
|
 Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence. Monday: [math]\displaystyle{ \pi }[/math] is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8. Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
 Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
 Monday: More Sturm comparisons, changing the independent variable. Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|

Add your name / see who's in!
|
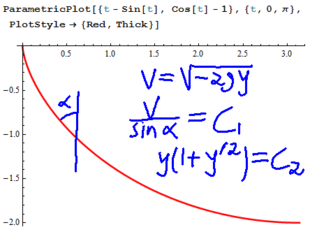
|
|
In Preparation
The information below is preliminary and cannot be trusted! (v)
Question 1. Show that if [math]\displaystyle{ y=y_1(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=0 }[/math], and [math]\displaystyle{ y=y_2(x) }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math], then for any constant [math]\displaystyle{ c }[/math], [math]\displaystyle{ y=cy_1+y_2 }[/math] is a solution of [math]\displaystyle{ y'+p(x)y=g(x) }[/math].
Question 2. Solve the following differential equations
- For [math]\displaystyle{ x\gt 0 }[/math], [math]\displaystyle{ xy'+2y=\sin x }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{1}{e^y-x} }[/math] with [math]\displaystyle{ y(1)=0 }[/math]; you may want to solve for [math]\displaystyle{ x }[/math] first.
- [math]\displaystyle{ xy'=\sqrt{1-y^2} }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{x-e^{-x}}{y+e^y} }[/math].
- [math]\displaystyle{ xdx+ye^{-x}dy=0 }[/math], with [math]\displaystyle{ y(0)=1 }[/math].
- [math]\displaystyle{ \frac{dy}{dx}=\frac{ax+b}{cx+d} }[/math], where [math]\displaystyle{ a,b,c,d }[/math] are arbitrary constants.
- [math]\displaystyle{ \frac{dy}{dx}=-\frac{ax+by}{bx+cy} }[/math], where [math]\displaystyle{ a,b,c }[/math] are arbitrary constants.
- [math]\displaystyle{ 0=(e^x\sin y + 3y)dx + (3(x+y)+e^x\cos y)dy }[/math].