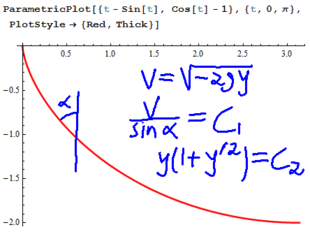12-267/Homework Assignment 2: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 3: | Line 3: | ||
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong. |
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, '''neatness counts!!''' You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong. |
||
'''Task 0.''' Identify yourself in the [[12-267/Class Photo|Class Photo]]! |
|||
| ⚫ | |||
| ⚫ | |||
# <math>x^2y^3+x(1+y^2)y'=0</math> (hint: try <math>\mu=x^\alpha y^\beta</math>). |
# <math>x^2y^3+x(1+y^2)y'=0</math> (hint: try <math>\mu=x^\alpha y^\beta</math>). |
||
# <math>dx+(\frac{x}{y}-\sin y)dy=0</math>. |
# <math>dx+(\frac{x}{y}-\sin y)dy=0</math>. |
||
| Line 11: | Line 13: | ||
# <math>\frac{dy}{dx}=\frac{2y+\sqrt{x^2-y^2}}{2x}</math>. |
# <math>\frac{dy}{dx}=\frac{2y+\sqrt{x^2-y^2}}{2x}</math>. |
||
''' |
'''Task 2.''' Let <math>M</math> and <math>N</math> be differentiable functions of <math>x</math> and <math>y</math>. |
||
# Show that if <math>\frac{N_x-M_y}{xM-yN}</math> depends only on <math>xy</math>, then the differential equation <math>Mdx+Ndy=0</math> has an integrating factor of the form <math>\mu(xy)</math>, where <math>\mu</math> is a function of a single variable. |
# Show that if <math>\frac{N_x-M_y}{xM-yN}</math> depends only on <math>xy</math>, then the differential equation <math>Mdx+Ndy=0</math> has an integrating factor of the form <math>\mu(xy)</math>, where <math>\mu</math> is a function of a single variable. |
||
# Find a condition on <math>M</math> and <math>N</math> that would imply that the differential equation <math>Mdx+Ndy=0</math> would have an integrating factor of the form <math>\mu(x+y)</math>, where <math>\mu</math> is a function of a single variable. |
# Find a condition on <math>M</math> and <math>N</math> that would imply that the differential equation <math>Mdx+Ndy=0</math> would have an integrating factor of the form <math>\mu(x+y)</math>, where <math>\mu</math> is a function of a single variable. |
||
''' |
'''Task 3.''' The equation <math>y'+p(x)y=q(x)y^n</math> is called a "Bernoulli Equation". |
||
# Explain why you already know how to solve the Bernoulli equation when <math>n=0</math> and when <math>n=1</math>. |
# Explain why you already know how to solve the Bernoulli equation when <math>n=0</math> and when <math>n=1</math>. |
||
# Show that if <math>n\neq0,1</math>, then the substitution <math>v=y^{1-n}</math> reduces the Bernoulli equation to an equation you already know how to solve. |
# Show that if <math>n\neq0,1</math>, then the substitution <math>v=y^{1-n}</math> reduces the Bernoulli equation to an equation you already know how to solve. |
||
# Solve the equation <math>x^2y'+2xy-y^3=0</math> (for <math>x>0</math>). |
# Solve the equation <math>x^2y'+2xy-y^3=0</math> (for <math>x>0</math>). |
||
''' |
'''Task 4.''' Find an example of a non-differentiable function which is nevertheless Lipschitz. |
||
Revision as of 16:00, 25 September 2012
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
This assignment is due at the tutorial on Tuesday October 2. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if the your readers will be having hard time deciphering your work they will give up and assume it is wrong.
Task 0. Identify yourself in the Class Photo!
Task 1. Solve the following differential equations:
- (hint: try ).
- .
- .
- (hint: consider trying and for good , ).
- with .
- .
Task 2. Let and be differentiable functions of and .
- Show that if depends only on , then the differential equation has an integrating factor of the form , where is a function of a single variable.
- Find a condition on and that would imply that the differential equation would have an integrating factor of the form , where is a function of a single variable.
Task 3. The equation is called a "Bernoulli Equation".
- Explain why you already know how to solve the Bernoulli equation when and when .
- Show that if , then the substitution reduces the Bernoulli equation to an equation you already know how to solve.
- Solve the equation (for ).
Task 4. Find an example of a non-differentiable function which is nevertheless Lipschitz.