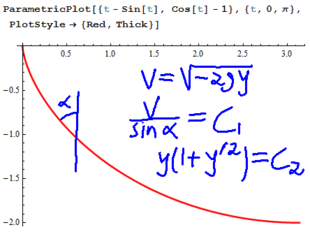| Additions to this web site no longer count towards good deed points.
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 10
|
About This Class.  Monday: Introduction and the Brachistochrone. Monday: Introduction and the Brachistochrone.  Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes. Tuesday: More on the Brachistochrone, administrative issues. Tuesday Notes.  Friday: Some basic techniques: first order linear equations. Friday: Some basic techniques: first order linear equations.
|
| 2
|
Sep 17
|
 Monday: Separated equations, escape velocities. HW1. Monday: Separated equations, escape velocities. HW1.  Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations. Tuesday: Escape velocities, changing source and target coordinates, homogeneous equations.  Friday: Reverse engineering separated and exact equations. Friday: Reverse engineering separated and exact equations.
|
| 3
|
Sep 24
|
 Monday: Solving exact equations, integration factors. HW2. Monday: Solving exact equations, integration factors. HW2.  Tuesday: Statement of the Fundamental Theorem. Class Photo. Tuesday: Statement of the Fundamental Theorem. Class Photo.  Friday: Proof of the Fundamental Theorem. Friday: Proof of the Fundamental Theorem.
|
| 4
|
Oct 1
|
 Monday: Last notes on the fundamental theorem. HW3. Monday: Last notes on the fundamental theorem. HW3.  Tuesday Hour 1: The chain law, examples of variational problems. Tuesday Hour 1: The chain law, examples of variational problems.  Tuesday Hour 2: Deriving Euler-Lagrange. Tuesday Hour 2: Deriving Euler-Lagrange.  Friday: Reductions of Euler-Lagrange. Friday: Reductions of Euler-Lagrange.
|
| 5
|
Oct 8
|
Monday is thanksgiving.  Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4. Tuesday: Lagrange multiplyers and the isoperimetric inequality. HW4.  Friday: More Lagrange multipliers, numerical methods. Friday: More Lagrange multipliers, numerical methods.
|
| 6
|
Oct 15
|
 Monday: Euler and improved Euler. Monday: Euler and improved Euler.  Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods. Tuesday: Evaluating the local error, Runge-Kutta, and a comparison of methods.  Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs. Friday: Numerical integration, high order constant coefficient homogeneous linear ODEs.
|
| 7
|
Oct 22
|
 Monday: Multiple roots, reduction of order, undetermined coefficients. Monday: Multiple roots, reduction of order, undetermined coefficients.  Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday. Tuesday: From systems to matrix exponentiation. HW5. Term Test on Friday.
|
| 8
|
Oct 29
|
 Monday: The basic properties of matrix exponentiation. Monday: The basic properties of matrix exponentiation.  Tuesday: Matrix exponentiation: examples. Tuesday: Matrix exponentiation: examples.  Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class Friday: Phase Portraits. HW6. Nov 4 was the last day to drop this class
|
| 9
|
Nov 5
|
 Monday: Non-homogeneous systems. Monday: Non-homogeneous systems.  Tuesday: The Catalan numbers, power series, and ODEs. Tuesday: The Catalan numbers, power series, and ODEs.  Friday: Global existence for linear ODEs, the Wronskian. Friday: Global existence for linear ODEs, the Wronskian.
|
| 10
|
Nov 12
|
Monday-Tuesday is UofT November break. HW7.  Friday: Series solutions for Friday: Series solutions for  . .
|
| 11
|
Nov 19
|
 Monday: Monday:  is irrational, more on the radius of convergence. is irrational, more on the radius of convergence.  Tuesday (class): Airy's equation, Fuchs' theorem. Tuesday (class): Airy's equation, Fuchs' theorem.  Tuesday (tutorial): Regular singular points. HW8. Tuesday (tutorial): Regular singular points. HW8.  Friday: Discussion of regular singular points.. Friday: Discussion of regular singular points..
|
| 12
|
Nov 26
|
 Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF). Monday: Frobenius series by computer. Qualitative Analysis Handout (PDF).  Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9. Tuesday: The basic oscillation theorem. Handout on the Frobenius Method. HW9.  Friday: Non-oscillation, Sturm comparison. Friday: Non-oscillation, Sturm comparison.
|
| 13
|
Dec 3
|
 Monday: More Sturm comparisons, changing the independent variable. Monday: More Sturm comparisons, changing the independent variable.  Tuesday: Amplitudes of oscillations. Last class was on Tuesday! Tuesday: Amplitudes of oscillations. Last class was on Tuesday!
|
| F1
|
Dec 10
|
|
| F2
|
Dec 17
|
The Final Exam (time, place, style, office hours times)
|
| Register of Good Deeds
|

Add your name / see who's in!
|
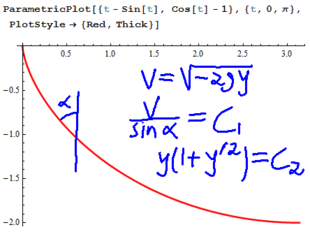
|
|
This assignment is due in class on Friday November 23. Here and everywhere, neatness counts!! You may be brilliant and you may mean just the right things, but if your readers have a hard time deciphering your work they will give up and assume it is wrong.
Task 1. Find the radius of convergence of the series
 .
. .
. near
near  .
.
Task 2. Solve the equation  with
with  and
and  using power series up to and including the coefficient of
using power series up to and including the coefficient of  . Then compare your result with the Taylor expansion of the exact solution.
. Then compare your result with the Taylor expansion of the exact solution.
Task 3. Find the recurrence relation defining the power series solutions of the following equations:
 with
with  and
and  .
. with
with  and
and  .
. with
with  and
and  .
.
Task 4. In view of the theorem about convergence of power series solutions (Fuchs' theorem), give a lower bound on the radius of convergence of the series solution of the equation  near
near  .
.
Task 5.
- Find a recurrence relation satisfied by
 .
.
- Find a differential equation satisfied by
 .
.
- Solve that equation to determine
 in general, and
in general, and  in particular.
in particular.
|
|
Dror's notes above / Student's notes below
|
|
Solutions Vsbdthrsh