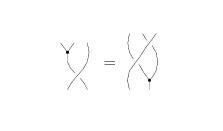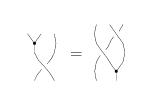User:Jana/06-1350-HW4

The Generators

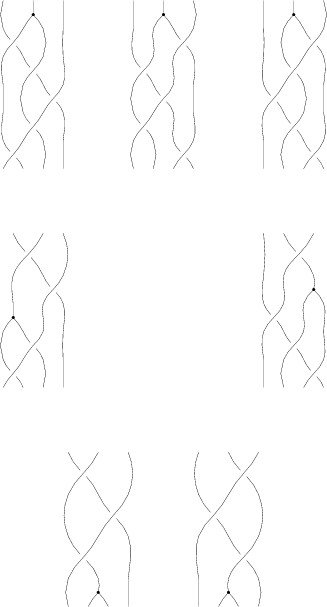
Our generators are [math]\displaystyle{ T }[/math], [math]\displaystyle{ R }[/math], [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ B^{\pm} }[/math]:

Picture
Generator	[math]\displaystyle{ T }[/math]	[math]\displaystyle{ R }[/math]	[math]\displaystyle{ \Phi }[/math]	[math]\displaystyle{ B^+ }[/math]	[math]\displaystyle{ B^- }[/math]
Perturbation	[math]\displaystyle{ t }[/math]	[math]\displaystyle{ r }[/math]	[math]\displaystyle{ \varphi }[/math]	[math]\displaystyle{ b^+ }[/math]	[math]\displaystyle{ b^- }[/math]

The Relations

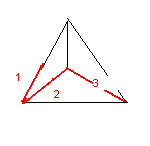
The Reidemeister Move R2 (Andy's)

The following version of R2 was the easiest to use to build my original [math]\displaystyle{ \Phi }[/math] around [math]\displaystyle{ \Phi }[/math] syzygy:

In formulas, this is

[math]\displaystyle{ 1 = (123)^\star B^- (132)^\star B^+. }[/math]

Linearized and written in functional form, this becomes

[math]\displaystyle{ \rho_2(x_1,x_2,x_3) = - b^-(x_1,x_2,x_3) - b^+(x_1,x_3,x_2). }[/math]

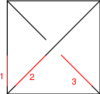
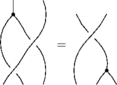
The Reidemeister Move R3

The picture (with three sides of the shielding removed) is

In formulas, this is

[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ }[/math].

Linearized and written in functional form, this becomes

[math]\displaystyle{ \rho_3(x_1, x_2, x_3, x_4) = }[/math]	[math]\displaystyle{ b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) }[/math]
	[math]\displaystyle{ - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3). }[/math]

R4

This Reidemeister move has a number of forms. I will put two here, both in linearized functional form. The two following were copied from Andy.

R4c

[math]\displaystyle{ \rho_4c(x_1, x_2, x_3, x_4) = }[/math]	[math]\displaystyle{ b^+(x_1,x_2,x_3) + \phi(x_1+x_2,x_3+x_4,x_4) }[/math]
	[math]\displaystyle{ - \phi(x_1+x_2+x_3,x_3+x_4,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_3+x_4,x_4). }[/math]

R4d

[math]\displaystyle{ \rho_4d(x_1, x_2, x_3, x_4) = }[/math]	[math]\displaystyle{ b^-(x_1,x_2,x_3) + \phi(x_1+x_2,x_3+x_4,x_4) }[/math]
	[math]\displaystyle{ - \phi(x_1+x_2+x_3,x_3+x_4,x_4) - b^-(x_1,x_2,x_4) - b^-(x_1+x_4,x_3+x_4,x_4). }[/math]

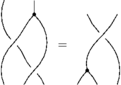
To establish the syzygy below, I needed two versions of R4. First:

In formulas, this is

[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star \Phi = (1123)^\star \Phi (1233)^\star B^+ }[/math].

Linearized and written in functional form, this becomes

[math]\displaystyle{ \rho_{4a}(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + \phi(x_1,x_3,x_4) - \phi(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_3+x_4). }[/math]

Second:

In formulas, this is

[math]\displaystyle{ (1123)^\star B^+ (1203)^\star B^+ (1231)^\star \Phi = (1230)^\star \Phi (1223)^\star B^+ }[/math].

Linearized and written in functional form, this becomes

[math]\displaystyle{ \rho_{4b}(x_1,x_2,x_3,x_4) = b^+(x_1+x_2,x_3,x_4) + b^+(x_1,x_2,x_4) + \phi(x_1+x_4,x_2,x_3) - \phi(x_1,x_2,x_3) - b^+(x_1,x_2+x_3,x_4). }[/math]

Are these independent, or can they be shown to be equivalent using other relations?

The Syzygies

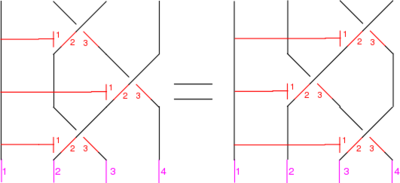
The "B around B" Syzygy

The picture, with all shielding removed, is

(Drawn with Inkscape) (note that lower quality pictures are also acceptable)

The functional form of this syzygy is

[math]\displaystyle{ BB(x_1,x_2,x_3,x_4,x_5) = }[/math]	[math]\displaystyle{ \rho_3(x_1, x_2, x_3, x_5) + \rho_3(x_1 + x_5, x_2, x_3, x_4) - \rho_3(x_1 + x_2, x_3, x_4, x_5) }[/math]
	[math]\displaystyle{ - \rho_3(x_1, x_2, x_4, x_5) - \rho_3(x_1 + x_4, x_2, x_3, x_5) - \rho_3(x_1, x_2, x_3, x_4) }[/math]
	[math]\displaystyle{ + \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5). }[/math]

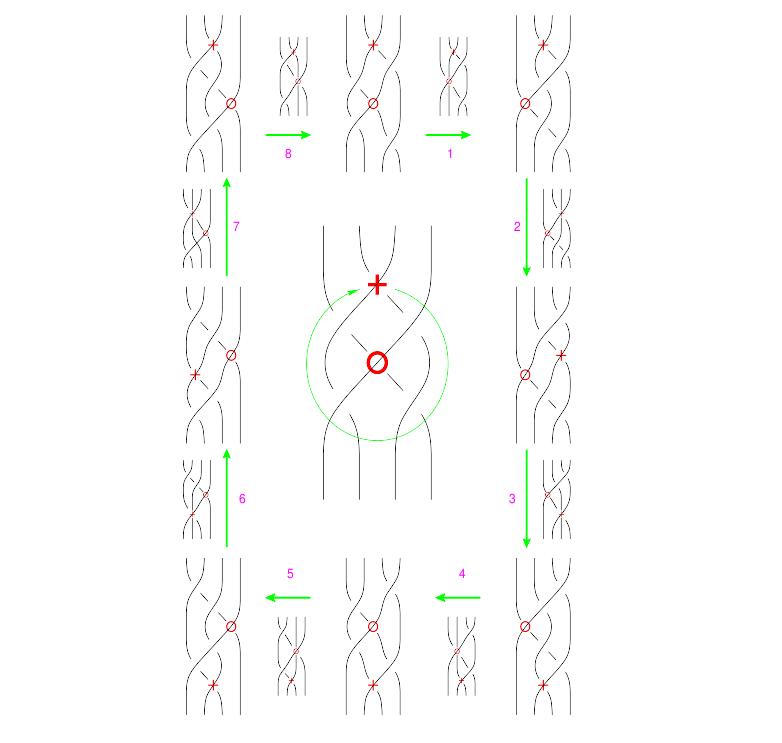
The "[math]\displaystyle{ \Phi }[/math] around B" Syzygy (By Andy)

The picture, with all shielding (and any other helpful notations) removed, is

(Drawn with Asymptote, Syzygies in Asymptote)

The functional form of this syzygy is

[math]\displaystyle{ \Phi B(x_1,x_2,x_3,x_4,x_5) = }[/math]	[math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_5) + \rho_{4a}(x_1+x_5,x_2,x_3,x_4) + \rho_{4b}(x_1+x_2,x_3,x_4,x_5) }[/math]
	[math]\displaystyle{ - \rho_3(x_1,x_2,x_3+x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4) }[/math]
	[math]\displaystyle{ - \rho_{4b}(x_1,x_3,x_4,x_5) + \rho_3(x_1+x_3,x_2,x_4,x_5). }[/math]

Phi around Phi

A Mathematica Verification

The following simulated Mathematica session proves that for our single relation and single syzygy, [math]\displaystyle{ d^2=0 }[/math]. Copy paste it into a live Mathematica session to see that it's right!

In[1]:=

d1 = { rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] }; d2 = { BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] };

In[3]:=	BAroundB[x1, x2, x3, x4, x5] /. d2
Out[3]=	- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] + rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4]

In[4]:=	BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
Out[4]=	0