Fields 2009 Finite Type Invariants Proposal
This is a part of a proposal for a 2009 Knot Theory Program at the Fields Institute.
What is a Universal Finite Type Invariant?
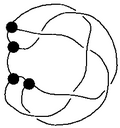
Given a graph [math]\displaystyle{ \Gamma }[/math] ("the skeleton"), let [math]\displaystyle{ {\mathcal K}(\Gamma) }[/math] denote the set of all "knottings" of [math]\displaystyle{ \Gamma }[/math] - the set of all embeddings of [math]\displaystyle{ \Gamma }[/math] into [math]\displaystyle{ {\mathbb R}^3 }[/math] considered modulo isotopy. So if [math]\displaystyle{ \Gamma }[/math] is a circle, [math]\displaystyle{ {\mathcal K}(\Gamma) }[/math] is an ordinary knot. If it is a union of circles, [math]\displaystyle{ {\mathcal K}(\Gamma) }[/math] is a link, and if it is, say, a tetrahedron, [math]\displaystyle{ {\mathcal K}(\Gamma) }[/math] will contain, for example, the knotted graph shown on the right.
A universal finite type invariant (using a rather broad definition) is a family of invariants [math]\displaystyle{ \{Z_\Gamma:{\mathcal K}(\Gamma)\to{\mathcal A}(\Gamma)\} }[/math], one for each skeleton [math]\displaystyle{ \Gamma }[/math], valued in some specific family of linear spaces [math]\displaystyle{ {\mathcal A}(\Gamma) }[/math] one for each [math]\displaystyle{ \Gamma }[/math]. The spaces [math]\displaystyle{ {\mathcal A}(\Gamma) }[/math] are themselves defined in terms of graphs along with some linear algebra, but since we don't need the details here, we won't show them. A certain "universality" property is expected to hold, but again, we don't need it right now so we won't discuss it.