| #
|
Week of...
|
Links
|
| 1
|
Jan 9
|
About, Notes, HW1
|
| 2
|
Jan 16
|
HW2, Notes
|
| 3
|
Jan 23
|
HW3, Photo, Notes
|
| 4
|
Jan 30
|
HW4, Notes
|
| 5
|
Feb 6
|
HW5, Notes
|
| 6
|
Feb 13
|
On TT, Notes
|
| R
|
Feb 20
|
Reading week
|
| 7
|
Feb 27
|
Term Test (and solution)
|
| 8
|
Mar 5
|
HW6, Notes
|
| 9
|
Mar 12
|
HW7, Notes
|
| 10
|
Mar 19
|
HW8, Notes, RC (PDF)
|
| 11
|
Mar 26
|
HW9, Notes
|
| 12
|
Apr 2
|
FT, HW10, Notes
|
| 13
|
Apr 9
|
Notes
|
| S
|
Apr 14-25
|
Study Period: blackboards
|
| F
|
Apr 28
|
Final
|

Add your name / see who's in!
|
| Register of Good Deeds
|
|
Announcements go here
The statement appearing here, which is a weak version of the full fundamental theorem of Galois theory, is taken from Gallian's book and is meant to match our discussion in class. The proof is taken from Hungerford's book, except modified to fit our notations and conventions and simplified as per our weakened requirements.
Here and everywhere below our base field  will be a field of characteristic 0.
will be a field of characteristic 0.
Statement
Theorem. Let  be a splitting field over
be a splitting field over  . Then there is a bijective correspondence between the set
. Then there is a bijective correspondence between the set  of intermediate field extensions
of intermediate field extensions  lying between
lying between  and
and  and the set
and the set  of subgroups
of subgroups  of the Galois group
of the Galois group  of the original extension
of the original extension  :
:
 .
.
The bijection is given by mapping every intermediate extension  to the subgroup
to the subgroup  of elements in
of elements in  that preserve
that preserve  ,
,
 ,
,
and reversely, by mapping every subgroup  of
of  to its fixed field
to its fixed field  :
:
 .
.
This correspondence has the following further properties:
- It is inclusion-reversing: if
 then
then  and if
and if  then
then  .
.
- It is degree/index respecting:
![{\displaystyle [E:K]=|\operatorname {Gal} (E/K)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c44a48df52c6cd4e1cf197de461b438c3270fd) and
and ![{\displaystyle [K:F]=[\operatorname {Gal} (E/F):\operatorname {Gal} (E/K)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e40beb2ae7daa66244aff7daefbafd6cdeabf6) .
.
- Splitting fields correspond to normal subgroups: If
 in
in  is the splitting field of a polynomial in
is the splitting field of a polynomial in ![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216) then
then  is normal in
is normal in  and
and  .
.
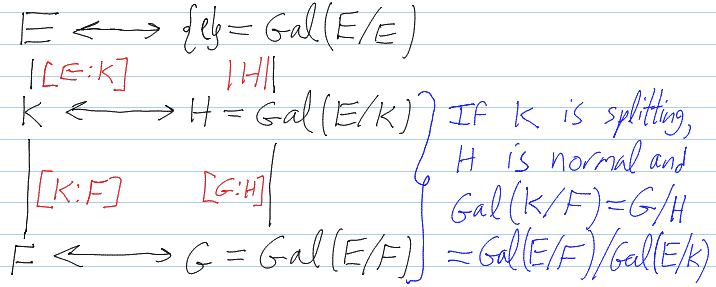
The Fundamental Theorem of Galois Theory, all in one.
Lemmas
The four lemmas below belong to earlier chapters but we skipped them in class (the last one was also skipped by Gallian).
Zeros of Irreducible Polynomials
Lemma 1. An irreducible polynomial over a field of characteristic 0 has no multiple roots.
Proof. See the proof of Theorem 20.6 on page 362 of Gallian's book. 
Uniqueness of Splitting Fields
Lemma 2. Let  be an isomorphism of fields, let
be an isomorphism of fields, let ![{\displaystyle f_{1}\in F_{1}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74ad8d86b493f3d09284b389e3ca4e4d101aaadf) be a polynomial and let
be a polynomial and let  , and let
, and let  and
and  be splitting fields for
be splitting fields for  and
and  over
over  and
and  , respectively. Then there is an isomorphism
, respectively. Then there is an isomorphism  (generally not unique) that extends
(generally not unique) that extends  .
.
Proof. See the proof of Theorem 20.4 on page 360 of Gallian's book. 
The Primitive Element Theorem
The celebrated "Primitive Element Theorem" is just a lemma for us:
Lemma 3. Let  and
and  be algebraic elements of some extension
be algebraic elements of some extension  of
of  . Then there exists a single element
. Then there exists a single element  of
of  so that
so that  . (And so by induction, every finite extension of
. (And so by induction, every finite extension of  is "simple", meaning, is generated by a single element, called "a primitive element" for that extension).
is "simple", meaning, is generated by a single element, called "a primitive element" for that extension).
Proof. See the proof of Theorem 21.6 on page 375 of Gallian's book. 
Splitting Fields are Good at Splitting
Lemma 4. (Compare with Hungerford's Theorem 10.15 on page 355). If  is a splitting field of some polynomial
is a splitting field of some polynomial  over
over  and some irreducible polynomial
and some irreducible polynomial ![{\displaystyle p\in F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a3455e0a007d78c63b1dc8e435af11a6b61642) has a root
has a root  in
in  , then
, then  splits in
splits in  .
.
Proof. Let  be a splitting field of
be a splitting field of  over
over  . We need to show that if
. We need to show that if  is a root of
is a root of  in
in  , then
, then  (so all the roots of
(so all the roots of  are in
are in  and hence
and hence  splits in
splits in  ). Consider the two extensions
). Consider the two extensions
 and
and  .
.
The "smaller fields"  and
and  in these two extensions are isomorphic as they both arise by adding a root of the same irreducible polynomial (
in these two extensions are isomorphic as they both arise by adding a root of the same irreducible polynomial ( ) to the base field
) to the base field  . The "larger fields"
. The "larger fields"  and
and  in these two extensions are both the splitting fields of the same polynomial (
in these two extensions are both the splitting fields of the same polynomial ( ) over the respective "small fields", as
) over the respective "small fields", as  is a splitting extension for
is a splitting extension for  and we can use the sub-lemma below. Thus by the uniqueness of splitting extensions (lemma 2), the isomorphism between
and we can use the sub-lemma below. Thus by the uniqueness of splitting extensions (lemma 2), the isomorphism between  and
and  extends to an isomorphism between
extends to an isomorphism between  and
and  , and in particular these two fields are isomorphic and so
, and in particular these two fields are isomorphic and so ![{\displaystyle [E:F]=[E(v):F]=[E(w):F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a24a256eb6de75a1dacd3d13f35be8efadfd320) . Since all the degrees involved are finite it follows from the last equality and from
. Since all the degrees involved are finite it follows from the last equality and from ![{\displaystyle [E(w):F]=[E(w):E][E:F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf9b7193b8fa07c797b1af0959c6d9b4b7762d55) that
that ![{\displaystyle [E(w):E]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d20b4e55660f62291fdc09da38821619ef10a0) and therefore
and therefore  . Therefore
. Therefore  .
. 
Sub-lemma. If  is a splitting extension of some polynomial
is a splitting extension of some polynomial ![{\displaystyle f\in F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ccbe5f3f86529d2b1b617a852f0368e16bba2d0) and
and  is an element of some larger extension
is an element of some larger extension  of
of  , then
, then  is also a splitting extension of
is also a splitting extension of  .
.
Proof. Let  be all the roots of
be all the roots of  in
in  . Then they remain roots of
. Then they remain roots of  in
in  , and since
, and since  completely splits already in
completely splits already in  , these are all the roots of
, these are all the roots of  in
in  . So
. So
 ,
,
and  is obtained by adding all the roots of
is obtained by adding all the roots of  to
to  .
. 
Proof of The Fundamental Theorem
The Bijection
Proof of  . More precisely, we need to show that if
. More precisely, we need to show that if  is an intermediate field between
is an intermediate field between  and
and  , then
, then  . The inclusion
. The inclusion  is easy, so we turn to prove the other inclusion. Let
is easy, so we turn to prove the other inclusion. Let  be an element of
be an element of  which is not in
which is not in  . We need to show that there is some automorphism
. We need to show that there is some automorphism  for which
for which  ; if such a
; if such a  exists it follows that
exists it follows that  and this implies the other inclusion. So let
and this implies the other inclusion. So let  be the minimal polynomial of
be the minimal polynomial of  over
over  . It is not of degree 1; if it was, we'd have that
. It is not of degree 1; if it was, we'd have that  contradicting the choice of
contradicting the choice of  . By lemma 4 and using the fact that
. By lemma 4 and using the fact that  is a splitting extension, we know that
is a splitting extension, we know that  splits in
splits in  , so
, so  contains all the roots of
contains all the roots of  . Over a field of characteristic 0 irreducible polynomials cannot have multiple roots (lemma 1) and hence
. Over a field of characteristic 0 irreducible polynomials cannot have multiple roots (lemma 1) and hence  must have at least one other root; call it
must have at least one other root; call it  . Since
. Since  and
and  have the same minimal polynomial over
have the same minimal polynomial over  , we know that
, we know that  and
and  are isomorphic; furthermore, there is an isomorphism
are isomorphic; furthermore, there is an isomorphism  so that
so that  yet
yet  . But
. But  is a splitting field of some polynomial
is a splitting field of some polynomial  over
over  and hence also over
and hence also over  and over
and over  . By the uniqueness of splitting fields (lemma 2), the isomorphism
. By the uniqueness of splitting fields (lemma 2), the isomorphism  can be extended to an isomorphism
can be extended to an isomorphism  ; i.e., to an automorphism of
; i.e., to an automorphism of  . but then
. but then  so
so  , yet
, yet  , as required.
, as required. 
Proof of  . More precisely we need to show that if
. More precisely we need to show that if  is a subgroup of the Galois group of
is a subgroup of the Galois group of  over
over  , then
, then  . The inclusion
. The inclusion  is easy. Note that
is easy. Note that  is finite since we've proven previously that Galois groups of finite extensions are finite and hence
is finite since we've proven previously that Galois groups of finite extensions are finite and hence  is finite. We will prove the following sequence of inequalities:
is finite. We will prove the following sequence of inequalities:
![{\displaystyle |H|\leq |\operatorname {Gal} (E/E_{H})|\leq [E:E_{H}]\leq |H|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96ffe5b29c1554f6b894a0c96f4269a84687b53)
This sequence and the finiteness of  imply that these quantities are all equal and since
imply that these quantities are all equal and since  it follows that
it follows that  as required.
as required.
The first inequality above follows immediately from the inclusion  .
.
By the Primitive Element Theorem (Lemma 3) we know that there is some element  so that
so that  . Let
. Let  be the minimal polynomial of
be the minimal polynomial of  over
over  . Distinct elements of
. Distinct elements of  map
map  to distinct roots of
to distinct roots of  , but
, but  has exactly
has exactly  roots. Hence
roots. Hence ![{\displaystyle |\operatorname {Gal} (E/E_{H})|\leq \deg p=[E:E_{H}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b87dc680a98caf9fd774e870cac71a68a0fa3c72) , proving the second inequality above.
, proving the second inequality above.
Let  be an enumeration of all the elements of
be an enumeration of all the elements of  , let
, let  (with
(with  as above), and let
as above), and let  be the polynomial
be the polynomial
 .
.
Clearly, ![{\displaystyle f\in E[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27b9340143e517d54bd068478c34f11db925016) . Furthermore, if
. Furthermore, if  , then left multiplication by
, then left multiplication by  permutes the
permutes the  's (this is always true in groups), and hence the sequence
's (this is always true in groups), and hence the sequence  is a permutation of the sequence
is a permutation of the sequence  , hence
, hence
 ,
,
and hence ![{\displaystyle f\in E_{H}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5edef9ce94234e3fc6d1717113f139dfe7d1c67) . Clearly
. Clearly  , so
, so  , so
, so ![{\displaystyle [E:E_{H}]=\deg p\leq \deg f=n=|H|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260f03cc2e78f96e758549476d640939be674ee6) , proving the third inequality above.
, proving the third inequality above. 
The Properties
Property 1. If  then
then  and if
and if  then
then  .
.
Proof of Property 1. Easy. 
Property 2. ![{\displaystyle [E:K]=|\operatorname {Gal} (E/K)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c44a48df52c6cd4e1cf197de461b438c3270fd) and
and ![{\displaystyle [K:F]=[\operatorname {Gal} (E/F):\operatorname {Gal} (E/K)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e40beb2ae7daa66244aff7daefbafd6cdeabf6) .
.
Proof of Property 2. If  , then
, then ![{\displaystyle |\operatorname {Gal} (E/K)|=|\operatorname {Gal} (E/E_{H})|=[E:E_{H}]=[E:K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f427ddcf1ee3a4e1c14a84b10a3b12f47ab03b20) as was shown within the proof of
as was shown within the proof of  . But every
. But every  is
is  for some
for some  , so
, so ![{\displaystyle |\operatorname {Gal} (E/K)|=[E:K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0089bc8be3ca20621ca2725e4cb413139b25c) for every
for every  between
between  and
and  . The second equality follows from the first and from the multiplicativity of the degree/order/index in towers of extensions and in towers of groups:
. The second equality follows from the first and from the multiplicativity of the degree/order/index in towers of extensions and in towers of groups:
![{\displaystyle [K:F]={\frac {[E:F]}{[E:K]}}={\frac {|\operatorname {Gal} (E/F)|}{|\operatorname {Gal} (E/K)|}}=[\operatorname {Gal} (E/F):\operatorname {Gal} (E/K)].\quad \Box }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e0026f7c5b4c2409b85fd4049c8315f9649c4a)
Property 3. If  in
in  is the splitting field of a polynomial in
is the splitting field of a polynomial in ![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216) then
then  is normal in
is normal in  and
and  .
.
Proof of Property 3. We will define a surjective (onto) group homomorphism  whose kernel is
whose kernel is  . This shows that
. This shows that  is normal in
is normal in  (kernels of homomorphisms are always normal) and then by the first isomorphism theorem for groups, we'll have that
(kernels of homomorphisms are always normal) and then by the first isomorphism theorem for groups, we'll have that  .
.
Let  be in
be in  and let
and let  be an element of
be an element of  . Let
. Let  be the minimal polynomial of
be the minimal polynomial of  in
in ![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216) . Since
. Since  is a splitting field, lemma 4 implies that
is a splitting field, lemma 4 implies that  splits in
splits in ![{\displaystyle K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9) , and hence all the other roots of
, and hence all the other roots of  are also in
are also in  . As
. As  is a root of
is a root of  , it follows that
, it follows that  and hence
and hence  . But since
. But since  is an isomorphism,
is an isomorphism, ![{\displaystyle [\sigma (K):F]=[K:F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db763793f3462d90979c59370a529683a661e522) and hence
and hence  . Hence the restriction
. Hence the restriction  of
of  to
to  is an automorphism of
is an automorphism of  , so we can define
, so we can define  .
.
Clearly,  is a group homomorphism. The kernel of
is a group homomorphism. The kernel of  is those automorphisms of
is those automorphisms of  whose restriction to
whose restriction to  is the identity. That is, it is
is the identity. That is, it is  . Finally, as
. Finally, as  is a splitting extension, so is
is a splitting extension, so is  . So every automorphism of
. So every automorphism of  extends to an automorphism of
extends to an automorphism of  by the uniqueness statement for splitting extensions (lemma 2). But this means that
by the uniqueness statement for splitting extensions (lemma 2). But this means that  is onto.
is onto. 


















![{\displaystyle [E:K]=|\operatorname {Gal} (E/K)|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/65c44a48df52c6cd4e1cf197de461b438c3270fd)
![{\displaystyle [K:F]=[\operatorname {Gal} (E/F):\operatorname {Gal} (E/K)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93e40beb2ae7daa66244aff7daefbafd6cdeabf6)

![{\displaystyle F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/39bc9f9d8679fc385df3bccf9694283b796f3216)

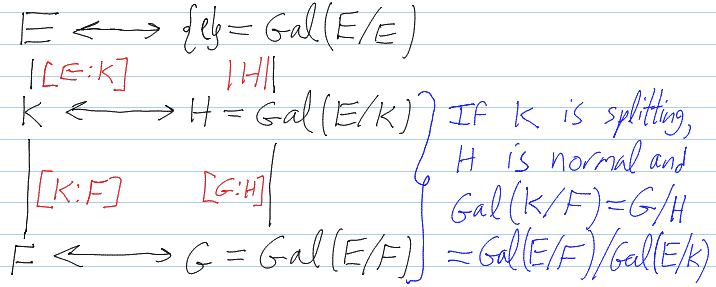


![{\displaystyle f_{1}\in F_{1}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/74ad8d86b493f3d09284b389e3ca4e4d101aaadf)














![{\displaystyle p\in F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/05a3455e0a007d78c63b1dc8e435af11a6b61642)











![{\displaystyle [E:F]=[E(v):F]=[E(w):F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a24a256eb6de75a1dacd3d13f35be8efadfd320)
![{\displaystyle [E(w):F]=[E(w):E][E:F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cf9b7193b8fa07c797b1af0959c6d9b4b7762d55)
![{\displaystyle [E(w):E]=1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a4d20b4e55660f62291fdc09da38821619ef10a0)

![{\displaystyle f\in F[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0ccbe5f3f86529d2b1b617a852f0368e16bba2d0)



























![{\displaystyle |H|\leq |\operatorname {Gal} (E/E_{H})|\leq [E:E_{H}]\leq |H|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b96ffe5b29c1554f6b894a0c96f4269a84687b53)






![{\displaystyle |\operatorname {Gal} (E/E_{H})|\leq \deg p=[E:E_{H}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b87dc680a98caf9fd774e870cac71a68a0fa3c72)



![{\displaystyle f\in E[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a27b9340143e517d54bd068478c34f11db925016)






![{\displaystyle f\in E_{H}[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b5edef9ce94234e3fc6d1717113f139dfe7d1c67)


![{\displaystyle [E:E_{H}]=\deg p\leq \deg f=n=|H|}](https://wikimedia.org/api/rest_v1/media/math/render/svg/260f03cc2e78f96e758549476d640939be674ee6)


![{\displaystyle |\operatorname {Gal} (E/K)|=|\operatorname {Gal} (E/E_{H})|=[E:E_{H}]=[E:K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f427ddcf1ee3a4e1c14a84b10a3b12f47ab03b20)
![{\displaystyle |\operatorname {Gal} (E/K)|=[E:K]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/95b0089bc8be3ca20621ca2725e4cb413139b25c)
![{\displaystyle [K:F]={\frac {[E:F]}{[E:K]}}={\frac {|\operatorname {Gal} (E/F)|}{|\operatorname {Gal} (E/K)|}}=[\operatorname {Gal} (E/F):\operatorname {Gal} (E/K)].\quad \Box }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a5e0026f7c5b4c2409b85fd4049c8315f9649c4a)


![{\displaystyle K[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8a9e6c2ac2830d6a9abe078b47450777c41d69a9)



![{\displaystyle [\sigma (K):F]=[K:F]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db763793f3462d90979c59370a529683a661e522)




