06-240/Classnotes For Tuesday December 5

06-240/Navigation Panel   # Week of... Notes and Links 1 Sep 11 About, Tue, HW1, Putnam, Thu 2 Sep 18 Tue, HW2, Thu 3 Sep 25 Tue, HW3, Photo, Thu 4 Oct 2 Tue, HW4, Thu 5 Oct 9 Tue, HW5, Thu 6 Oct 16 Why?, Iso, Tue, Thu 7 Oct 23 Term Test, Thu (double) 8 Oct 30 Tue, HW6, Thu 9 Nov 6 Tue, HW7, Thu 10 Nov 13 Tue, HW8, Thu 11 Nov 20 Tue, HW9, Thu 12 Nov 27 Tue, HW10, Thu 13 Dec 4 On the final, Tue, Thu F Dec 11 Final: Dec 13 2-5PM at BN3, Exam Forum Register of Good Deeds Add your name / see who's in! edit the panel

Our remaining goal for this semester is to study the following theorem:

Theorem. Let [math]\displaystyle{ A }[/math] be an [math]\displaystyle{ n\times n }[/math] matrix (with entries in some field [math]\displaystyle{ F }[/math]) and let [math]\displaystyle{ \chi_A(\lambda):=\det(A-\lambda I) }[/math] be the characteristic polynomial of [math]\displaystyle{ A }[/math]. Assume [math]\displaystyle{ \chi_A }[/math] has [math]\displaystyle{ n }[/math] distinct roots [math]\displaystyle{ \lambda_1\ldots\lambda_n }[/math], that is, [math]\displaystyle{ A }[/math] has [math]\displaystyle{ n }[/math] distinct eigenvalues [math]\displaystyle{ \lambda_1\ldots\lambda_n }[/math], and let [math]\displaystyle{ v_1,\ldots,v_n }[/math] be corresponding eigenvectors, so that [math]\displaystyle{ Av_i=\lambda_iv_i }[/math] for all [math]\displaystyle{ 1\leq i\leq n }[/math]. Let [math]\displaystyle{ D }[/math] be the diagonal matrix that has [math]\displaystyle{ \lambda_1 }[/math] through [math]\displaystyle{ \lambda_n }[/math] on its main diagonal (in order) and let [math]\displaystyle{ P }[/math] be the matrix whose columns are these eigenvectors: [math]\displaystyle{ P:=(v_1|v_2|\cdots|v_n) }[/math]. Then [math]\displaystyle{ P }[/math] is invertible and the following equalities hold:

1. [math]\displaystyle{ D=P^{-1}AP }[/math] and [math]\displaystyle{ A=PDP^{-1} }[/math].
2. For any positive integer [math]\displaystyle{ k }[/math] we have [math]\displaystyle{ A^k=PD^kP^{-1} }[/math] and [math]\displaystyle{ D^k=\begin{pmatrix}\lambda_1^k&&0\\&\ddots&\\0&&\lambda_n^k\end{pmatrix} }[/math].
3. Likewise if [math]\displaystyle{ F={\mathbb R} }[/math] and [math]\displaystyle{ \exp(B):=\sum_{k=0}^\infty\frac{B^k}{k!} }[/math] then [math]\displaystyle{ \exp(A)=P\exp(D)P^{-1} }[/math] and [math]\displaystyle{ \exp(D)=\begin{pmatrix}e^{\lambda_1}&&0\\&\ddots&\\0&&e^{\lambda_n}\end{pmatrix} }[/math].

Order of the proceedings.

1. Assuming P is invertible, a proof of 1.
2. Proof of 2.
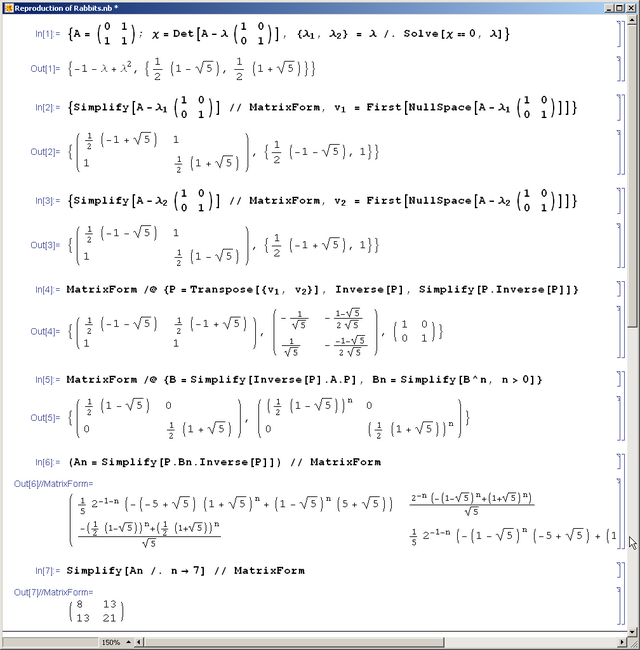
3. Example - the "reproduction of rabbits" matrix [math]\displaystyle{ A=\begin{pmatrix}0&1\\1&1\end{pmatrix} }[/math] (see the mathematica session below).
4. Discussion of 3.
5. The relationship with linear transformations and changes of basis.
6. [math]\displaystyle{ v_1 }[/math] thorough [math]\displaystyle{ v_n }[/math] form a basis and [math]\displaystyle{ P }[/math] is invertible.