HandoutBrowser.js
This is the web home of HandoutBrowser.js, a short JavaScript program I wrote that allows for programmed scrolling through a "handout" (really, just an image of any kind) within a web browser.
To do
- Document everything.
- Study anti-aliasing.
- Use cookies to save state.
- Allow "backwards" capture rectangles, and capture rectangles with negative coordinates.
- Consider an image-map-based quick navigator.
- Solve Firefox inaccuracies.
- Improve logging.
- Make an "embedded" version.
- Add a scroll bar for the log display.
- Fix the "handout only" key to show the highest available resolution.
- Implement "copyToClipboard" for views and log also for firefox and chrome. (Probably not worth the bother).
Download and Setup
Download the latest (top or near top) JavaScript and HTML files from the versions table below, save the two files in the same directory, and rename and modify the HTML file to suit your requirements.
| Version of | JavaScript | HTML | Comments |
|---|---|---|---|
| GWU-1203 | HandoutBrowser.js
|
beta.html | Bug fix. |
| Colombia-1107 | HandoutBrowser.js
|
Stonehenge.html | Minor tweaks. |
| Tennessee-1103 | HandoutBrowser.js
|
CC.html | Minor bug fix. |
| Toronto-110110 | HandoutBrowser.js
|
GT.html | Minor provision for interaction with dbnvp added. |
| Chicago-1009 | HandoutBrowser.js
|
axpb.html, 18C.html | "Copy to clipboard" of views and log implemented, but only for explorer. |
| Montpellier-1006 | HandoutBrowser.js
|
m1.html | Another logging bug fixed. |
| Luminy-1004 | HandoutBrowser.js
|
18C.html | Minor bugs fixed (one by Scott Morrison), resized log display. |
| Fields-0911 | HandoutBrowser.js
|
Hilbert13th.html | Log entry skipped if [math]\displaystyle{ \Delta t\lt 2\mbox{sec} }[/math].. |
| Bonn-0908 | HandoutBrowser.js
|
KV.html | Minor tweak and bug fix. |
| HUJI-090727 | HandoutBrowser.js
|
KV.html | Persistent logging (using cookies). |
| Mathcamp-0907 | HandoutBrowser.js
|
hardest.html, NCGE.html | Added "talk timer", work on logging. |
| Paris-0906 | HandoutBrowser.js
|
KV.html | Bug fixed. |
| Trieste-0905 | HandoutBrowser.js
|
KV.html, TheGrandScheme.html, Day4.html | Bug fixed, default for "views". |
| KSU-090407 | HandoutBrowser.js
|
hardest.html | Settable "glide_mode", hyperbolic gliding, minor tweaks. A bit buggy. |
| PSU-090205 | HandoutBrowser.js
|
3x4.html | Easier setup, "next view". |
| Oberwolfach-0805 | HandoutBrowser.js
|
Ober.html | Lower resolution while gliding, minor touches. |
| UofT-GS-071023 | HandoutBrowser.js
|
NCGE.html | Double buffering following Morrison's spiders talk, support for multiple slide resolutions, minor touches. |
| Fields-0709 | HandoutBrowser.js
|
VeryPlanar.html | Pull down goto menu, 4 text levels. |
| Hanoi-0708 | HandoutBrowser.js
|
FollowingLin.html | Mouse dragging, capture rectangle. |
| Tianjin-0707 | HandoutBrowser.js
|
FollowingLin.html | First working version. |
Documentation
Largely, this project is undocumented other than the hints that appear in the browser window itself. The exception is what I had to write down in order not to forget it myself.
Timer and Logging Functions
The key "b" swaps the text mode and turns on logging, if it was off. The key "l" displays the current log and suspends logging. The key "v" clears the current log and suspends logging. The timer is shown (unless textmode is 0) iff logging is on.
Users
- http://tqft.net/math/nzms/ by Scott Morrison.
- http://tqft.net/spiders by Scott Morrison.
- http://tqft.net/hanoi by Scott Morrison.
Competitors
Prezi came later, and may be more user friendly. I didn't look at it seriously yet.
A Related Math Problem
The HandoutBrowser.js project is not about math, but about displaying math (or other things, just as well). Yet some truly lovely math found its way in, and I once wrote a short note explaining it, or rather, posing it. That note also explains, even if briefly, why I bother with the HandoutBrowser.js project. Here it is.
The problem I'm about to describe came from a completely practical place. For reasons of ideology and convenience, often I give my talks out of a single-page densely printed handout that contains all major formulas and pictures I use in my talk. One page is what fits in one hour, and any member of my audience can read ahead and back and is not forced to follow my exact pace as would be the case in a PowerPoint presentation (and is not bumped off the moment her internal pace slightly deviates from mine).
The talk itself then consists of projecting the handout using a data projector, zooming in into it, and moving my viewport from one formula or picture to another, while supplying the accompanying vocals. My little technical problem is then, how to best slide the viewport from one view to the next, while generating the least motion blur in the process, so that my audience will be able to follow and find the present viewport in the printed copy? Here's another variant:
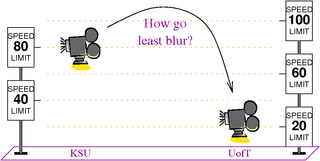
Question. Assume the Earth is flat. We want to fly a virtual video camera from a kilometer above the Kansas State campus (so that the whole thing is in sight) to a kilometer above the University of Toronto campus (so that the whole thing is in sight) in 10 seconds or less, so that the resulting movie will have the least blur. Clearly, we shouldn't fly at a constant elevation, for a camera moving so fast so close to the ground will suffer immense motion blur. Instead, we should fly up and thus zoom out, then move sideways fast but while we're far, and then zoom back in again. But what's the precise optimal path? And what should our speed be at any point along that path?
You should figure out the solution yourself, or read about it here (hit "n" a number of times to move around the handout), or watch a video explaining it ![]() here. Whichever you do, I'm very proud of this problem - it is the hardest practical math problem I ever had to deal with personally and the solution is a beautiful introduction to some wonderful mathematics.
here. Whichever you do, I'm very proud of this problem - it is the hardest practical math problem I ever had to deal with personally and the solution is a beautiful introduction to some wonderful mathematics.