Welcome to Math 1100!
(additions to this web site no longer count towards good deed points)
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 8
|
About This Class; Monday - Non Commutative Gaussian Elimination; Thursday - the category of groups, automorphisms and conjugations, images and kernels.
|
| 2
|
Sep 15
|
Monday - coset spaces, isomorphism theorems; Thursday - simple groups, Jordan-Holder decomposition series.
|
| 3
|
Sep 22
|
Monday - alternating groups, group actions, The Simplicity of the Alternating Groups, HW1, HW 1 Solutions, Class Photo; Thursday - group actions, Orbit-Stabilizer Thm, Class Equation.
|
| 4
|
Sep 29
|
Monday - Cauchy's Thm, Sylow 1; Thursday - Sylow 2.
|
| 5
|
Oct 6
|
Monday - Sylow 3, semi-direct products, braids; HW2; HW 2 Solutions; Thursday - braids, groups of order 12, Braids
|
| 6
|
Oct 13
|
No class Monday (Thanksgiving); Thursday - groups of order 12 cont'd.
|
| 7
|
Oct 20
|
Term Test; Term Test Solutions on Monday, HW3; HW 3 Solutions; Thursday - solvable groups, rings: defn's & examples.
|
| 8
|
Oct 27
|
Monday - functors, Cayley-Hamilton Thm, ideals, iso thm 1; Thursday - iso thms 2-4, integral domains, maximal ideals, One Theorem, Three Corollaries, Five Weeks
|
| 9
|
Nov 3
|
Monday - prime ideals, primes & irreducibles, UFD's, Euc.Domain PID, Thursday - Noetherian rings, PID PID, Thursday - Noetherian rings, PID UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions
|
| 10
|
Nov 10
|
Monday - R is a PID iff R has a D-H norm, R-modules, direct sums, every f.g. module is given by a presentation matrix, Thursday - row & column reductions plus, existence part of Thm 1 in 1t3c5w handout.
|
| 11
|
Nov 17
|
Monday-Tuesday is UofT's Fall Break, HW5, Thursday - 1t3c5w handout cont'd, JCF Tricks & Programs handout
|
| 12
|
Nov 24
|
Monday - JCF Tricks & Programs cont'd, tensor products, Thursday - tensor products cont'd
|
| 13
|
Dec 1
|
End-of-Course Schedule; Monday - tensor products finale, extension/reduction of scalars, uniqueness part of Thm 1 in 1t3c5w, localization & fields of fractions; Wednesday is a "makeup Monday"!; Notes for Studying for the Final Exam Glossary of terms
|
| F
|
Dec 15
|
The Final Exam
|
| Register of Good Deeds
|
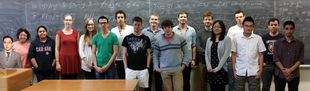
Add your name / see who's in!
|

See Non Commutative Gaussian Elimination
|
|
This assignment is extended from class time on Wednesday, December 3, 2014 (a "virtual Monday" and the last day of the semester) to the end of Monday, December 8 in Dror's mailbox.
Solve the following questions
Problem 1. Let  be a module over a PID
be a module over a PID  . Assume that
. Assume that  is isomorphic to
is isomorphic to  , with
, with  non-zero non-units and with
non-zero non-units and with  . Assume also that
. Assume also that  is isomorphic to
is isomorphic to  , with
, with  non-zero non-units and with
non-zero non-units and with  . Prove that
. Prove that  , that
, that  , and that
, and that  for each
for each  .
.
Problem 2. Let  and
and  be primes in a PID
be primes in a PID  such that
such that  , let
, let  denote the operation of "multiplication by
denote the operation of "multiplication by  ", acting on any
", acting on any  -module
-module  , and let
, and let  and
and  be positive integers.
be positive integers.
- For each of the
 -modules
-modules  ,
,  , and
, and  , determine
, determine  and
and  .
.
- Explain why this approach for proving the uniqueness in the structure theorem for finitely generated modules fails.
Problem 3. (comprehensive exam, 2009) Find the tensor product of the ![{\displaystyle {\mathbb {C} }[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b320388ef42719220c79fd0800935e2d490956a) modules
modules ![{\displaystyle {\mathbb {C} }[t,t^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/434476c9681bd15ca4ca484f4752703e07dd1c00) ("Laurent polynomials in
("Laurent polynomials in  ") and
") and  (here
(here  acts on
acts on  as
as  ).
).
Problem 4. (from Selick) Show that if  is a PID and
is a PID and  is a multiplicative subset of
is a multiplicative subset of  then
then  is also a PID.
is also a PID.
Definition. The "rank" of a module  over a (commutative) domain
over a (commutative) domain  is the maximal number of
is the maximal number of  -linearly-independent elements of
-linearly-independent elements of  . (Linear dependence and independence is defined as in vector spaces).
. (Linear dependence and independence is defined as in vector spaces).
Definition. An element  of a module
of a module  over a commutative domain
over a commutative domain  is called a "torsion element" if there is a non-zero
is called a "torsion element" if there is a non-zero  such that
such that  . Let
. Let  denote the set of all torsion elements of
denote the set of all torsion elements of  . (Check that
. (Check that  is always a submodule of
is always a submodule of  , but don't bother writing this up). A module
, but don't bother writing this up). A module  is called a "torsion module" if
is called a "torsion module" if  .
.
Problem 5. (Dummit and Foote, page 468) Let  be a module over a commutative domain
be a module over a commutative domain  .
.
- Suppose that
 has rank
has rank  and that
and that  is a maximal set of linearly independent elements of
is a maximal set of linearly independent elements of  . Show that
. Show that  is isomorphic to
is isomorphic to  and that
and that  is a torsion module.
is a torsion module.
- Conversely show that if
 contains a submodule
contains a submodule  which is isomorphic to
which is isomorphic to  for some
for some  , and so that
, and so that  is torsion, then the rank of
is torsion, then the rank of  is
is  .
.
Problem 6. (see also Dummit and Foote, page 469) Show that the ideal  in
in ![{\displaystyle R={\mathbb {Z} }[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11975a9e1f0612ee86f0dd0c135d6255ef9a6987) , regarded as a module over
, regarded as a module over  , is finitely generated but cannot be written in the form
, is finitely generated but cannot be written in the form  .
.

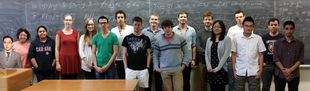























![{\displaystyle {\mathbb {C} }[t]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8b320388ef42719220c79fd0800935e2d490956a)
![{\displaystyle {\mathbb {C} }[t,t^{-1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/434476c9681bd15ca4ca484f4752703e07dd1c00)

















![{\displaystyle R={\mathbb {Z} }[x]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/11975a9e1f0612ee86f0dd0c135d6255ef9a6987)
