08-401/Homework Assignment 10 (and last!): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1: | Line 1: | ||
{{08-401/Navigation}} |
{{08-401/Navigation}} |
||
{{In Preparation}} |
|||
Ok, it is time to acknowledge defeat. We've come to within a few hundred yards of the summit (just the few pages of the "[[08-401/The Fundamental Theorem|Fundamental Theorem]]" handout, to be precise, and about two further lemmas from the book), the summit is clear in sight, yet we are not going to make it to the top. It is better now to retreat to base camp, and just talk a bit about where we have been and the little further, where we haven't been and will not go this time. |
|||
===Reading=== |
|||
Read chapter 32 of Gallian's book ('''6th edition''') and the "[[08-401/The Fundamental Theorem|Fundamental Theorem]]" handout three times: |
|||
* First time as if you were reading a novel - quickly and without too much attention to detail, just to learn what the main keywords and concepts and goals are. |
|||
* Second time like you were studying for an exam on the subject - slowly and not skipping anything, verifying every little detail. |
|||
* And then a third time, again at a quicker pace, to remind yourself of the bigger picture all those little details are there to paint. |
|||
So next class will be a light class. I will tie a few loose ends and return a few debts, and perhaps briefly mention one of the key points we are still missing, but I will not attempt to push everything that is left into the remaining three hours. We will also discuss the final exam and the schedule leading up to it. |
|||
===Doing=== |
|||
Solve problems ??? in chapter 32 of Gallian's book ('''6th edition'''), but submit only the solutions of the problems marked with the letter "S". |
|||
This assignment will likewise be light. Your only tasks are to read the "[[08-401/The Fundamental Theorem|Fundamental Theorem]]" handout to get an overall impression of its content, and to have fun with the Just for Fun questions below. Nothing to submit and no due date, and HW grades will be computed using your best 7 out of 9 grades, rather than 8 out of 10 (in the [[08-401/About This Class|About This Class]] document, I was careful to state that there wil be "about 10 homework assignments", and not "exactly 10"). |
|||
===Due Date=== |
|||
This assignment is due in class on Wednesday April 9, 2008. |
|||
===Just for Fun=== |
===Just for Fun=== |
||
Latest revision as of 14:48, 3 April 2008
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Ok, it is time to acknowledge defeat. We've come to within a few hundred yards of the summit (just the few pages of the "Fundamental Theorem" handout, to be precise, and about two further lemmas from the book), the summit is clear in sight, yet we are not going to make it to the top. It is better now to retreat to base camp, and just talk a bit about where we have been and the little further, where we haven't been and will not go this time.
So next class will be a light class. I will tie a few loose ends and return a few debts, and perhaps briefly mention one of the key points we are still missing, but I will not attempt to push everything that is left into the remaining three hours. We will also discuss the final exam and the schedule leading up to it.
This assignment will likewise be light. Your only tasks are to read the "Fundamental Theorem" handout to get an overall impression of its content, and to have fun with the Just for Fun questions below. Nothing to submit and no due date, and HW grades will be computed using your best 7 out of 9 grades, rather than 8 out of 10 (in the About This Class document, I was careful to state that there wil be "about 10 homework assignments", and not "exactly 10").
Just for Fun
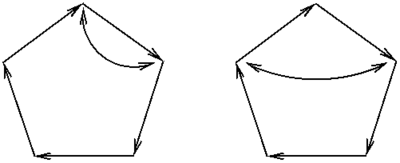
1. As done in class, prove that the following two "pentagonal rubik's style" combinatorial games are always solvable:
2. Which of the following three "hexagonal rubik's style" combinatorial games are always solvable?