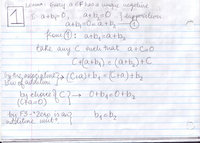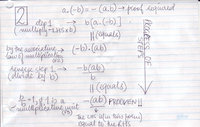06-240/Classnotes For Tuesday, September 12

06-240/Navigation Panel   # Week of... Notes and Links 1 Sep 11 About, Tue, HW1, Putnam, Thu 2 Sep 18 Tue, HW2, Thu 3 Sep 25 Tue, HW3, Photo, Thu 4 Oct 2 Tue, HW4, Thu 5 Oct 9 Tue, HW5, Thu 6 Oct 16 Why?, Iso, Tue, Thu 7 Oct 23 Term Test, Thu (double) 8 Oct 30 Tue, HW6, Thu 9 Nov 6 Tue, HW7, Thu 10 Nov 13 Tue, HW8, Thu 11 Nov 20 Tue, HW9, Thu 12 Nov 27 Tue, HW10, Thu 13 Dec 4 On the final, Tue, Thu F Dec 11 Final: Dec 13 2-5PM at BN3, Exam Forum Register of Good Deeds Add your name / see who's in! edit the panel

• PDF notes by User:Harbansb: September 12 Notes.
• If I have made an error in my notes, or you would like the editable OpenOffice file, feel free to e-mail me at harbansb@msn.com.
• September 12 Notes for re-uploading, please email at jeff.matskin@utoronto.ca
• PDF notes by User:Alla: Week 1 Lecture 1 notes
• Below are a couple of lemmata critical to the derivation we did in class - the Professor left this little work to the students:

Notes

The Real Numbers

The Real Numbers are a set (denoted by [math]\displaystyle{ \mathbb{R} }[/math]) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true:

[math]\displaystyle{ \mathbb{R}1 }[/math]: [math]\displaystyle{ \forall a, b\in \mathbb{R} }[/math] we have [math]\displaystyle{ a+b=b+a }[/math] and [math]\displaystyle{ a\cdot b=b\cdot a }[/math] (The Commutative Laws)

[math]\displaystyle{ \mathbb{R}2 }[/math]: [math]\displaystyle{ \forall a, b, c\in \mathbb{R} }[/math] we have [math]\displaystyle{ (a+b)+c=a+(b+c) }[/math] and [math]\displaystyle{ (a\cdot b)\cdot c=a\cdot (b\cdot c) }[/math] (The Associative Laws)

[math]\displaystyle{ \mathbb{R}3 }[/math]: [math]\displaystyle{ 0 }[/math] is an additive unit and [math]\displaystyle{ 1 }[/math] is a multiplicative unit (The Existence of Units/Identities)

[math]\displaystyle{ \mathbb{R}4 }[/math]: [math]\displaystyle{ \forall a\in \mathbb{R} \ \exists b\in \mathbb{R} \mbox{ s.t.} \ a+b=0 }[/math]

This is incomplete.