06-240/Classnotes For Tuesday December 5: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
m (Reverted edit of 213.185.1.179, changed back to last version by Drorbn) |
||
| Line 5: | Line 5: | ||
'''Theorem.''' Let <math>A</math> be an <math>n\times n</math> matrix (with entries in some field <math>F</math>) and let <math>\chi_A(\lambda):=\det(A-\lambda I)</math> be the characteristic polynomial of <math>A</math>. Assume <math>\chi_A</math> has <math>n</math> distinct roots <math>\lambda_1\ldots\lambda_n</math>, that is, <math>A</math> has <math>n</math> distinct eigenvalues <math>\lambda_1\ldots\lambda_n</math>, and let <math>v_1,\ldots,v_n</math> be corresponding eigenvectors, so that <math>Av_i=\lambda_iv_i</math> for all <math>1\leq i\leq n</math>. Let <math>D</math> be the diagonal matrix that has <math>\lambda_1</math> through <math>\lambda_n</math> on its main diagonal (in order) and let <math>P</math> be the matrix whose columns are these eigenvectors: <math>P:=(v_1|v_2|\cdots|v_n)</math>. Then <math>P</math> is invertible and the following equalities hold: |
'''Theorem.''' Let <math>A</math> be an <math>n\times n</math> matrix (with entries in some field <math>F</math>) and let <math>\chi_A(\lambda):=\det(A-\lambda I)</math> be the characteristic polynomial of <math>A</math>. Assume <math>\chi_A</math> has <math>n</math> distinct roots <math>\lambda_1\ldots\lambda_n</math>, that is, <math>A</math> has <math>n</math> distinct eigenvalues <math>\lambda_1\ldots\lambda_n</math>, and let <math>v_1,\ldots,v_n</math> be corresponding eigenvectors, so that <math>Av_i=\lambda_iv_i</math> for all <math>1\leq i\leq n</math>. Let <math>D</math> be the diagonal matrix that has <math>\lambda_1</math> through <math>\lambda_n</math> on its main diagonal (in order) and let <math>P</math> be the matrix whose columns are these eigenvectors: <math>P:=(v_1|v_2|\cdots|v_n)</math>. Then <math>P</math> is invertible and the following equalities hold: |
||
# <math>D=P^{-1}AP</math> and <math>A=PDP^{-1}</math>. |
# <math>D=P^{-1}AP</math> and <math>A=PDP^{-1}</math>. |
||
# For any positive integer <math>k</math> we have <math>A^k=PD^kP^{-1}</math> and <math>D^k=\begin{pmatrix}\lambda_1^k</math> |
# For any positive integer <math>k</math> we have <math>A^k=PD^kP^{-1}</math> and <math>D^k=\begin{pmatrix}\lambda_1^k&&0\\&\ddots&\\0&&\lambda_n^k\end{pmatrix}</math>. |
||
# Likewise if <math>F={\mathbb R}</math> and <math>\exp(B):=\sum_{k=0}^\infty\frac{B^k}{k!}</math> then <math>\exp(A)=P\exp(D)P^{-1}</math> and <math>\exp(D)=\begin{pmatrix}e^{\lambda_1}&&0\\&\ddots&\\0&&e^{\lambda_n}\end{pmatrix}</math>. |
|||
'''Order of the proceedings.''' |
|||
# Assuming P is invertible, a proof of 1. |
|||
# Proof of 2. |
|||
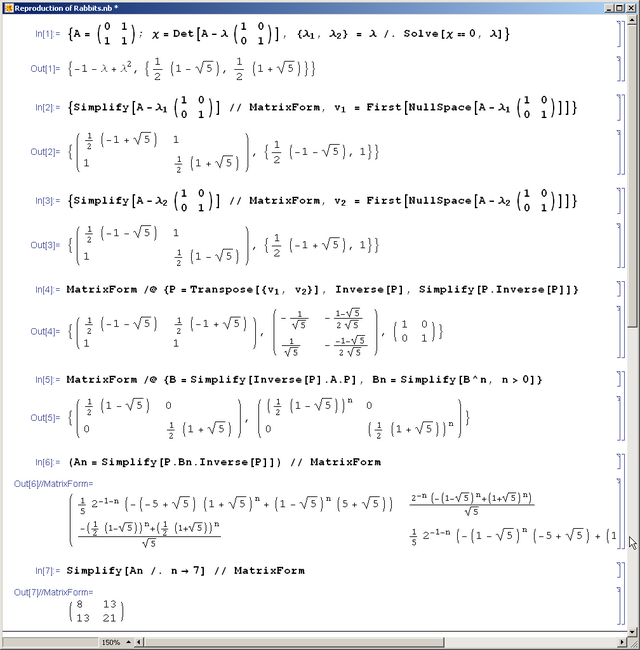
# Example - the "reproduction of rabbits" matrix <math>A=\begin{pmatrix}0&1\\1&1\end{pmatrix}</math> (see the mathematica session below). |
|||
# Discussion of 3. |
|||
# The relationship with linear transformations and changes of basis. |
|||
# <math>v_1</math> thorough <math>v_n</math> form a basis and <math>P</math> is invertible. |
|||
[[Image:06-240-Reproduction of Rabbits.png|center|640px]] |
|||
Latest revision as of 09:50, 28 May 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Our remaining goal for this semester is to study the following theorem:
Theorem. Let be an matrix (with entries in some field ) and let be the characteristic polynomial of . Assume has distinct roots , that is, has distinct eigenvalues , and let be corresponding eigenvectors, so that for all . Let be the diagonal matrix that has through on its main diagonal (in order) and let be the matrix whose columns are these eigenvectors: . Then is invertible and the following equalities hold:
- and .
- For any positive integer we have and .
- Likewise if and then and .
Order of the proceedings.
- Assuming P is invertible, a proof of 1.
- Proof of 2.
- Example - the "reproduction of rabbits" matrix (see the mathematica session below).
- Discussion of 3.
- The relationship with linear transformations and changes of basis.
- thorough form a basis and is invertible.