06-1350/Syzygies in Asymptote: Difference between revisions
(More writing.) |
(Added equations and corrected code.) |
||
| Line 15: | Line 15: | ||
b.add(phi,0); // Add a trivalent vertex that merges strands 0 and 1. |
b.add(phi,0); // Add a trivalent vertex that merges strands 0 and 1. |
||
// Strand 2 is now renumbered as strand 1. |
// Strand 2 is now renumbered as strand 1. |
||
b.draw() |
b.draw(); // Draw the resulting braid. |
||
</pre> |
</pre> |
||
When saved into an asy file, say <code>mybraid.asy</code> and run with Asymptote, the result is a picture: |
When saved into an asy file, say <code>mybraid.asy</code> and run with Asymptote, the result is a picture: |
||
[[Image:06-1350-mybraid.png|center]] |
|||
ADD PICTURE |
|||
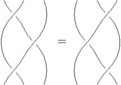
To define a relation, we first define two braids, and then stick them into a <code>Relation</code> structure. The below script generates an R3 relation. |
To define a relation, we first define two braids, and then stick them into a <code>Relation</code> structure. The below script generates an R3 relation. |
||
<pre> |
<pre> |
||
import syzygy; // Access the syzygy module. |
import syzygy; // Access the syzygy module. |
||
Braid l |
Braid l; // Define the left hand side of the relation. |
||
l.n=3; l.add(bp,0); l.add(bp,1); l.add(bp,0); |
l.n=3; l.add(bp,0); l.add(bp,1); l.add(bp,0); |
||
Braid r |
Braid r; // Define the right hand side of the relation. |
||
r.n=3; r.add(bp,1); |
r.n=3; r.add(bp,1); r.add(bp,0); r.add(bp,1); |
||
Relation r3; // Define a relation. |
Relation r3; // Define a relation. |
||
r3.lsym="\rho_3"; // Give the relation a name for when it is written in functional form. |
|||
r3.codename="rho3"; // Give the relation a name to used by Mathematica. |
|||
r3.lhs=l; r3.rhs=r; |
|||
r3.draw(); |
|||
</pre> |
</pre> |
||
When saved into an asy file and run, this draws the two sides of the relation. If TeX is installed, Asymptote will also put a lovely equals sign, typeset by TeX, between the two figures. |
When saved into an asy file and run, this draws the two sides of the relation. If TeX is installed, Asymptote will also put a lovely equals sign, typeset by TeX, between the two figures. |
||
[[Image:06-1350-R3-asy.png|center]] |
|||
ADD ANOTHER PICTURE |
|||
We can also get useful equations out of the relation. The method <code>r3.toFormula()</code> will produce a string that is the formula for the relation. |
We can also get useful equations out of the relation. The method <code>r3.toFormula()</code> will produce a string that is the formula for the relation. |
||
<pre> |
<pre> |
||
(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = |
|||
big ugly string |
|||
(1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ |
|||
</pre> |
</pre> |
||
This string can be written out to the standard output by <code>write(r3.toFormula())</code>. It can be written to a file by <code>file f=output("filename.txt"); write(f, r3.toFormula())</code>. The string is formatted so it can be put into TeX or a wiki page using math mode: |
This string can be written out to the standard output by <code>write(r3.toFormula())</code>. It can be written to a file by <code>file f=output("filename.txt"); write(f, r3.toFormula())</code>. The string is formatted so it can be put into TeX or a wiki page using math mode: |
||
<math> |
|||
ADD EQUATION |
|||
(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = |
|||
(1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ |
|||
</math> |
|||
The method <code>r3.toLinear()</code> produces the formula in linear form: |
The method <code>r3.toLinear()</code> produces the formula in linear form: |
||
<math> |
|||
ADD EQUATION |
|||
\rho_3(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3) |
|||
</math> |
|||
and <code>r3.toCode()</code> produces a version of the relation that can be used in Mathematica: |
and <code>r3.toCode()</code> produces a version of the relation that can be used in Mathematica: |
||
<pre> |
<pre> |
||
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] |
|||
ADD CODE |
|||
- bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] |
|||
</pre> |
</pre> |
||
| Line 78: | Line 85: | ||
</pre> |
</pre> |
||
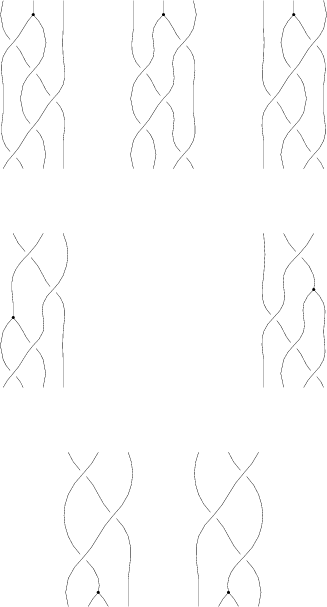
[[Image:06-1350-bbstart.png|center]] |
|||
ADD PICTURE |
|||
After skipping the lowest knot, we can apply R3 to the next three knots: |
After skipping the lowest knot, we can apply R3 to the next three knots: |
||
| Line 88: | Line 95: | ||
here <code>apply(r, b, k, n)</code> means we are applying the relation <code>r</code> to the braid <code>b</code> at the place in the braid found by counting <code>k</code> components up from the bottom component and <code>n</code> strands in from the leftmost strand. <code>apply</code> does not modify the original braid, but returns the result of applying the relation (stored here as <code>bb</code>): |
here <code>apply(r, b, k, n)</code> means we are applying the relation <code>r</code> to the braid <code>b</code> at the place in the braid found by counting <code>k</code> components up from the bottom component and <code>n</code> strands in from the leftmost strand. <code>apply</code> does not modify the original braid, but returns the result of applying the relation (stored here as <code>bb</code>): |
||
[[Image:06-1350-bbnext.png|center]] |
|||
ADD PICTURE |
|||
This went from the left hand side of the relation to the right hand side. To apply a relation in reverse, simply prefix it by a minus sign. For example <code>apply(-r3, bb, 1, 0)</code> will yield a braid equivalent to our original. When applying a relation, the script first checks that the one side of the relation matches that portion of the braid, and will give a (somewhat cryptic) error if the relation cannot be applied. |
This went from the left hand side of the relation to the right hand side. To apply a relation in reverse, simply prefix it by a minus sign. For example <code>apply(-r3, bb, 1, 0)</code> will yield a braid equivalent to our original. When applying a relation, the script first checks that the one side of the relation matches that portion of the braid, and will give a (somewhat cryptic) error if the relation cannot be applied. |
||
| Line 98: | Line 105: | ||
</pre> |
</pre> |
||
[[Image:06-1350-bbswap.png|center]] |
|||
ADD PICTURE |
|||
Remember that components are ordered from bottom to top, starting at 0. Again, the script checks to make sure the swap is valid (ie. changing the order of the two components, doesn't actually change the knot) and will issue an error if it isn't. |
Remember that components are ordered from bottom to top, starting at 0. Again, the script checks to make sure the swap is valid (ie. changing the order of the two components, doesn't actually change the knot) and will issue an error if it isn't. |
||
| Line 105: | Line 112: | ||
<pre> |
<pre> |
||
import syzygy; |
|||
lots of code |
|||
// Phi around B |
|||
Braid initial; |
|||
initial.n=4; |
|||
initial.add(bp,2); |
|||
initial.add(bp,0); |
|||
initial.add(bp,1); |
|||
initial.add(bp,0); |
|||
initial.add(bp,2); |
|||
initial.add(phi,1); |
|||
Syzygy pb; |
|||
pb.lsym="\Phi B"; |
|||
pb.codename="PhiAroundB"; |
|||
pb.initial=initial; |
|||
pb.apply(r3,1,0); |
|||
pb.apply(r4a,3,1); |
|||
pb.swap(2,3); |
|||
pb.apply(r4b,0,1); |
|||
pb.apply(-r3,1,0); |
|||
pb.apply(-r4a,0,0); |
|||
pb.swap(2,3); |
|||
pb.apply(-r4b,3,0); |
|||
pb.apply(r3,1,1); |
|||
pb.draw(); |
|||
</pre> |
|||
and the result |
|||
[[Image:06-1350-PhiAroundB.png|center]] |
|||
Again, like relations, we can use <code>pb.toLinear()</code> |
|||
{| align=center |
|||
|- |
|||
|<math>\Phi B(x_1,x_2,x_3,x_4,x_5) = </math> |
|||
|<math>\rho_3(x_1,x_2,x_3,x_5) + \rho_{4a}(x_1+x_5,x_2,x_3,x_4) + \rho_{4b}(x_1+x_2,x_3,x_4,x_5)</math> |
|||
|- |
|||
| |
|||
|<math>- \rho_3(x_1,x_2,x_3+x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4)</math> |
|||
|- |
|||
| |
|||
|<math>- \rho_{4b}(x_1,x_3,x_4,x_5) + \rho_3(x_1+x_3,x_2,x_4,x_5).</math> |
|||
|} |
|||
and <code>pb.toCode()</code> |
|||
<pre> |
|||
PhiAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho4a[x1 + x5, x2, x3, x4] |
|||
+ rho4b[x1 + x2, x3, x4, x5] - rho3[x1, x2, x3 + x4, x5] - rho4a[x1, x2, x3, x4] |
|||
- rho4b[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] |
|||
</pre> |
</pre> |
||
to give the formulas for the syzygies. |
|||
Revision as of 17:56, 4 December 2006
WARNING: These instructions are a work in progress and should be considered highly unreliable.
To use the syzygy script, first install Asymptote. Instructions for installing the program on several OSes is given in the documentation at the Asymptote website. The documentation also gives helpful instructions on how to run a script in Asymptote to produce a picture. Once installed, download syzygy.asy and put it in a directory where Asymptote can find it. You should also have (or install) a variant of TeX on your system, such as MiKTeX, so that Asymptote can typeset labels.
Once installed, we can draw a braid in Asymptote:
import syzygy; // Accesses the syzygy module.
Braid b; // Start a new braid.
b.n=3; // The braid has three strands.
// The strands are numbered left to right starting at 0.
b.add(bp,0); // Add a overcrossing component starting at strand 0,
// the leftmost strand.
b.add(bm,1); // Add an undercrossing starting at strand 1.
b.add(phi,0); // Add a trivalent vertex that merges strands 0 and 1.
// Strand 2 is now renumbered as strand 1.
b.draw(); // Draw the resulting braid.
When saved into an asy file, say mybraid.asy and run with Asymptote, the result is a picture:
To define a relation, we first define two braids, and then stick them into a Relation structure. The below script generates an R3 relation.
import syzygy; // Access the syzygy module. Braid l; // Define the left hand side of the relation. l.n=3; l.add(bp,0); l.add(bp,1); l.add(bp,0); Braid r; // Define the right hand side of the relation. r.n=3; r.add(bp,1); r.add(bp,0); r.add(bp,1); Relation r3; // Define a relation. r3.lsym="\rho_3"; // Give the relation a name for when it is written in functional form. r3.codename="rho3"; // Give the relation a name to used by Mathematica. r3.lhs=l; r3.rhs=r; r3.draw();
When saved into an asy file and run, this draws the two sides of the relation. If TeX is installed, Asymptote will also put a lovely equals sign, typeset by TeX, between the two figures.
We can also get useful equations out of the relation. The method r3.toFormula() will produce a string that is the formula for the relation.
(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+
This string can be written out to the standard output by write(r3.toFormula()). It can be written to a file by file f=output("filename.txt"); write(f, r3.toFormula()). The string is formatted so it can be put into TeX or a wiki page using math mode:
The method r3.toLinear() produces the formula in linear form:
and r3.toCode() produces a version of the relation that can be used in Mathematica:
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4]
- bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3]
A few relations, such as r3, are already defined in syzygy.asy but more should be added.
Now that we have relations, we can apply them to bigger braids. Let's start with the braid in the around B syzygy:
import syzygy; Braid b; b.n=4; b.add(bp,2); b.add(bp,0); b.add(bp,1); b.add(bp,0); b.add(bp,2); b.add(phi,1);
After skipping the lowest knot, we can apply R3 to the next three knots:
Braid bb=apply(r3, b, 1, 0);
here apply(r, b, k, n) means we are applying the relation r to the braid b at the place in the braid found by counting k components up from the bottom component and n strands in from the leftmost strand. apply does not modify the original braid, but returns the result of applying the relation (stored here as bb):
This went from the left hand side of the relation to the right hand side. To apply a relation in reverse, simply prefix it by a minus sign. For example apply(-r3, bb, 1, 0) will yield a braid equivalent to our original. When applying a relation, the script first checks that the one side of the relation matches that portion of the braid, and will give a (somewhat cryptic) error if the relation cannot be applied.
In our braids, the components are placed from bottom to top in a fixed order. Sometimes when building syzygies, it is neccessary to swap the order that these components occur. This is done by the swap method. For instance, starting from b, we can swap the two bottom crossings:
Braid swapped=b.swap(0,1);
Remember that components are ordered from bottom to top, starting at 0. Again, the script checks to make sure the swap is valid (ie. changing the order of the two components, doesn't actually change the knot) and will issue an error if it isn't.
One could manually apply relations and swaps, and make a whole bunch of braids, but it would be annoying to keep track of them all. Thankfully, the Syzygy structure does that for us. For example, here is the complete code for the around B syzygy:
import syzygy; // Phi around B Braid initial; initial.n=4; initial.add(bp,2); initial.add(bp,0); initial.add(bp,1); initial.add(bp,0); initial.add(bp,2); initial.add(phi,1); Syzygy pb; pb.lsym="\Phi B"; pb.codename="PhiAroundB"; pb.initial=initial; pb.apply(r3,1,0); pb.apply(r4a,3,1); pb.swap(2,3); pb.apply(r4b,0,1); pb.apply(-r3,1,0); pb.apply(-r4a,0,0); pb.swap(2,3); pb.apply(-r4b,3,0); pb.apply(r3,1,1); pb.draw();
and the result
Again, like relations, we can use pb.toLinear()
and pb.toCode()
PhiAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho4a[x1 + x5, x2, x3, x4] + rho4b[x1 + x2, x3, x4, x5] - rho3[x1, x2, x3 + x4, x5] - rho4a[x1, x2, x3, x4] - rho4b[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5]
to give the formulas for the syzygies.