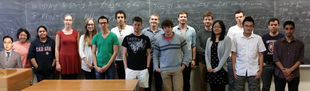14-1100/Homework Assignment 4

DBN: Classes: 2014-15: 14-1100/Navigation Welcome to Math 1100! (additions to this web site no longer count towards good deed points) # Week of... Notes and Links 1 Sep 8 About This Class; Monday - Non Commutative Gaussian Elimination; Thursday - the category of groups, automorphisms and conjugations, images and kernels. 2 Sep 15 Monday - coset spaces, isomorphism theorems; Thursday - simple groups, Jordan-Holder decomposition series. 3 Sep 22 Monday - alternating groups, group actions, The Simplicity of the Alternating Groups, HW1, HW 1 Solutions, Class Photo; Thursday - group actions, Orbit-Stabilizer Thm, Class Equation. 4 Sep 29 Monday - Cauchy's Thm, Sylow 1; Thursday - Sylow 2. 5 Oct 6 Monday - Sylow 3, semi-direct products, braids; HW2; HW 2 Solutions; Thursday - braids, groups of order 12, Braids 6 Oct 13 No class Monday (Thanksgiving); Thursday - groups of order 12 cont'd. 7 Oct 20 Term Test; Term Test Solutions on Monday, HW3; HW 3 Solutions; Thursday - solvable groups, rings: defn's & examples. 8 Oct 27 Monday - functors, Cayley-Hamilton Thm, ideals, iso thm 1; Thursday - iso thms 2-4, integral domains, maximal ideals, One Theorem, Three Corollaries, Five Weeks 9 Nov 3 Monday - prime ideals, primes & irreducibles, UFD's, Euc.Domain[math]\displaystyle{ \Rightarrow }[/math]PID, Thursday - Noetherian rings, PID[math]\displaystyle{ \Rightarrow }[/math]UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions 10 Nov 10 Monday - R is a PID iff R has a D-H norm, R-modules, direct sums, every f.g. module is given by a presentation matrix, Thursday - row & column reductions plus, existence part of Thm 1 in 1t3c5w handout. 11 Nov 17 Monday-Tuesday is UofT's Fall Break, HW5, Thursday - 1t3c5w handout cont'd, JCF Tricks & Programs handout 12 Nov 24 Monday - JCF Tricks & Programs cont'd, tensor products, Thursday - tensor products cont'd 13 Dec 1 End-of-Course Schedule; Monday - tensor products finale, extension/reduction of scalars, uniqueness part of Thm 1 in 1t3c5w, localization & fields of fractions; Wednesday is a "makeup Monday"!; Notes for Studying for the Final Exam Glossary of terms F Dec 15 The Final Exam Register of Good Deeds Add your name / see who's in! See Non Commutative Gaussian Elimination

This assignment is due at class time on Thursday, November 20, 2011.

Solve the following questions

Problem 1. (Klein's 1983 course)

1. Show that the ideal [math]\displaystyle{ I=\langle 3,\, x^3-x^2+2x-1\rangle }[/math] inside the ring [math]\displaystyle{ {\mathbb Z}[x] }[/math] is not principal.
2. Is [math]\displaystyle{ {\mathbb Z}[x]/I }[/math] a domain?

Problem 2. Prove that a ring [math]\displaystyle{ R }[/math] is a PID iff it is a UFD in which [math]\displaystyle{ \gcd(a,b)\in\langle a, b\rangle }[/math] for every non-zero [math]\displaystyle{ a,b\in R }[/math].

Problem 3. (Lang) Show that the ring [math]\displaystyle{ {\mathbb Z}[i]=\{a+ib\colon a,b\in{\mathbb Z}\}\subset{\mathbb C} }[/math] is a PID and hence a UFD. What are the units of that ring?

Problem 4. (Dummit and Foote) In [math]\displaystyle{ {\mathbb Z}[i] }[/math], find the greatest common divisor of [math]\displaystyle{ 85 }[/math] and [math]\displaystyle{ 1+13i }[/math], and express it as a linear combination of these two elements.

Problem 5. (Klein's 1983 course) Show that [math]\displaystyle{ {\mathbb Z}[\sqrt{10}] }[/math] is not a UFD.

Problem 6. (Hard!) Show that the quotient ring [math]\displaystyle{ {\mathbb Q}[x,y]/\langle x^2+y^2-1\rangle }[/math] is not a UFD.