06-240/Classnotes For Tuesday December 5: Difference between revisions
No edit summary |
m (Reverted edit of 213.185.1.179, changed back to last version by Drorbn) |
||
| Line 5: | Line 5: | ||
'''Theorem.''' Let <math>A</math> be an <math>n\times n</math> matrix (with entries in some field <math>F</math>) and let <math>\chi_A(\lambda):=\det(A-\lambda I)</math> be the characteristic polynomial of <math>A</math>. Assume <math>\chi_A</math> has <math>n</math> distinct roots <math>\lambda_1\ldots\lambda_n</math>, that is, <math>A</math> has <math>n</math> distinct eigenvalues <math>\lambda_1\ldots\lambda_n</math>, and let <math>v_1,\ldots,v_n</math> be corresponding eigenvectors, so that <math>Av_i=\lambda_iv_i</math> for all <math>1\leq i\leq n</math>. Let <math>D</math> be the diagonal matrix that has <math>\lambda_1</math> through <math>\lambda_n</math> on its main diagonal (in order) and let <math>P</math> be the matrix whose columns are these eigenvectors: <math>P:=(v_1|v_2|\cdots|v_n)</math>. Then <math>P</math> is invertible and the following equalities hold: |
'''Theorem.''' Let <math>A</math> be an <math>n\times n</math> matrix (with entries in some field <math>F</math>) and let <math>\chi_A(\lambda):=\det(A-\lambda I)</math> be the characteristic polynomial of <math>A</math>. Assume <math>\chi_A</math> has <math>n</math> distinct roots <math>\lambda_1\ldots\lambda_n</math>, that is, <math>A</math> has <math>n</math> distinct eigenvalues <math>\lambda_1\ldots\lambda_n</math>, and let <math>v_1,\ldots,v_n</math> be corresponding eigenvectors, so that <math>Av_i=\lambda_iv_i</math> for all <math>1\leq i\leq n</math>. Let <math>D</math> be the diagonal matrix that has <math>\lambda_1</math> through <math>\lambda_n</math> on its main diagonal (in order) and let <math>P</math> be the matrix whose columns are these eigenvectors: <math>P:=(v_1|v_2|\cdots|v_n)</math>. Then <math>P</math> is invertible and the following equalities hold: |
||
# <math>D=P^{-1}AP</math> and <math>A=PDP^{-1}</math>. |
# <math>D=P^{-1}AP</math> and <math>A=PDP^{-1}</math>. |
||
# For any positive integer <math>k</math> we have <math>A^k=PD^kP^{-1}</math> and <math>D^k=\begin{pmatrix}\lambda_1^k</math> |
# For any positive integer <math>k</math> we have <math>A^k=PD^kP^{-1}</math> and <math>D^k=\begin{pmatrix}\lambda_1^k&&0\\&\ddots&\\0&&\lambda_n^k\end{pmatrix}</math>. |
||
# Likewise if <math>F={\mathbb R}</math> and <math>\exp(B):=\sum_{k=0}^\infty\frac{B^k}{k!}</math> then <math>\exp(A)=P\exp(D)P^{-1}</math> and <math>\exp(D)=\begin{pmatrix}e^{\lambda_1}&&0\\&\ddots&\\0&&e^{\lambda_n}\end{pmatrix}</math>. |
|||
'''Order of the proceedings.''' |
|||
# Assuming P is invertible, a proof of 1. |
|||
# Proof of 2. |
|||
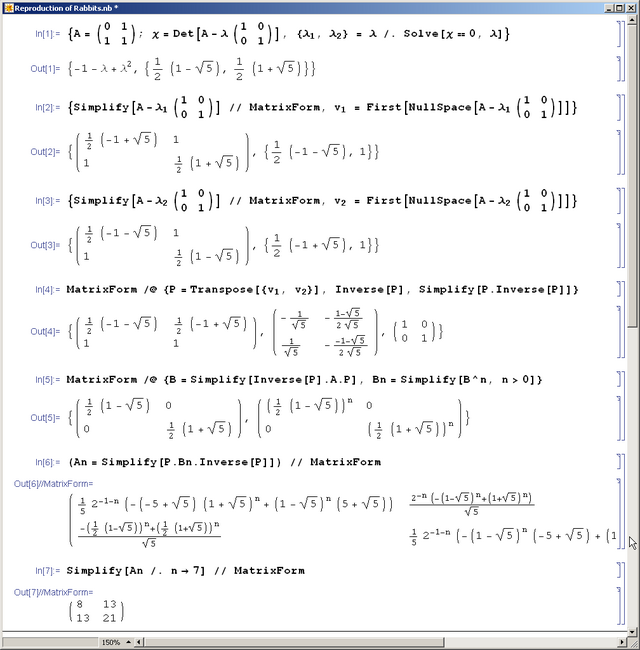
# Example - the "reproduction of rabbits" matrix <math>A=\begin{pmatrix}0&1\\1&1\end{pmatrix}</math> (see the mathematica session below). |
|||
# Discussion of 3. |
|||
# The relationship with linear transformations and changes of basis. |
|||
# <math>v_1</math> thorough <math>v_n</math> form a basis and <math>P</math> is invertible. |
|||
[[Image:06-240-Reproduction of Rabbits.png|center|640px]] |
|||
Latest revision as of 09:50, 28 May 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
Our remaining goal for this semester is to study the following theorem:
Theorem. Let [math]\displaystyle{ A }[/math] be an [math]\displaystyle{ n\times n }[/math] matrix (with entries in some field [math]\displaystyle{ F }[/math]) and let [math]\displaystyle{ \chi_A(\lambda):=\det(A-\lambda I) }[/math] be the characteristic polynomial of [math]\displaystyle{ A }[/math]. Assume [math]\displaystyle{ \chi_A }[/math] has [math]\displaystyle{ n }[/math] distinct roots [math]\displaystyle{ \lambda_1\ldots\lambda_n }[/math], that is, [math]\displaystyle{ A }[/math] has [math]\displaystyle{ n }[/math] distinct eigenvalues [math]\displaystyle{ \lambda_1\ldots\lambda_n }[/math], and let [math]\displaystyle{ v_1,\ldots,v_n }[/math] be corresponding eigenvectors, so that [math]\displaystyle{ Av_i=\lambda_iv_i }[/math] for all [math]\displaystyle{ 1\leq i\leq n }[/math]. Let [math]\displaystyle{ D }[/math] be the diagonal matrix that has [math]\displaystyle{ \lambda_1 }[/math] through [math]\displaystyle{ \lambda_n }[/math] on its main diagonal (in order) and let [math]\displaystyle{ P }[/math] be the matrix whose columns are these eigenvectors: [math]\displaystyle{ P:=(v_1|v_2|\cdots|v_n) }[/math]. Then [math]\displaystyle{ P }[/math] is invertible and the following equalities hold:
- [math]\displaystyle{ D=P^{-1}AP }[/math] and [math]\displaystyle{ A=PDP^{-1} }[/math].
- For any positive integer [math]\displaystyle{ k }[/math] we have [math]\displaystyle{ A^k=PD^kP^{-1} }[/math] and [math]\displaystyle{ D^k=\begin{pmatrix}\lambda_1^k&&0\\&\ddots&\\0&&\lambda_n^k\end{pmatrix} }[/math].
- Likewise if [math]\displaystyle{ F={\mathbb R} }[/math] and [math]\displaystyle{ \exp(B):=\sum_{k=0}^\infty\frac{B^k}{k!} }[/math] then [math]\displaystyle{ \exp(A)=P\exp(D)P^{-1} }[/math] and [math]\displaystyle{ \exp(D)=\begin{pmatrix}e^{\lambda_1}&&0\\&\ddots&\\0&&e^{\lambda_n}\end{pmatrix} }[/math].
Order of the proceedings.
- Assuming P is invertible, a proof of 1.
- Proof of 2.
- Example - the "reproduction of rabbits" matrix [math]\displaystyle{ A=\begin{pmatrix}0&1\\1&1\end{pmatrix} }[/math] (see the mathematica session below).
- Discussion of 3.
- The relationship with linear transformations and changes of basis.
- [math]\displaystyle{ v_1 }[/math] thorough [math]\displaystyle{ v_n }[/math] form a basis and [math]\displaystyle{ P }[/math] is invertible.