06-240/Homework Assignment 6: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 4: | Line 4: | ||
* '''Solve''' problems 1, 2, <u>5</u>, 13, <u>17</u> and 18 on pages 74-76, problems 1, 5a, <u>5b</u>, 5c-g, 9, 15 and <u>16</u> on pages 84-86 and problems 1, 2, <u>3a</u> and 3b on pages 96-97, but submit only your solutions of the underlined problems. This assignment is due at the tutorials on Thursday November 9. |
* '''Solve''' problems 1, 2, <u>5</u>, 13, <u>17</u> and 18 on pages 74-76, problems 1, 5a, <u>5b</u>, 5c-g, 9, 15 and <u>16</u> on pages 84-86 and problems 1, 2, <u>3a</u> and 3b on pages 96-97, but submit only your solutions of the underlined problems. This assignment is due at the tutorials on Thursday November 9. |
||
* '''Just for fun.''' Decide if the vectors <math>\begin{pmatrix}8\\-3\end{pmatrix}</math> and <math>\begin{pmatrix}5\\-2\end{pmatrix}</math> are linearly dependent. |
|||
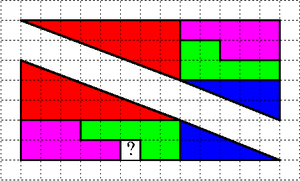
<center>'''How Can This Be?'''</center> |
|||
[[Image:How Can This Be.png|thumb|300px|center|Two congruent triangles are assembled using congruent pieces, yet one is bigger than the other]] |
|||
Latest revision as of 08:55, 2 November 2006
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
- Read sections 2.1 through 2.3 in our textbook. Remember that reading math isn't like reading a novel! If you read a novel and miss a few details most likely you'll still understand the novel. But if you miss a few details in a math text, often you'll miss everything that follows. So reading math takes reading and rereading and rerereading and a lot of thought about what you've read. Also, preread sections 2.4 and 2.5, just to get a feel for the future.
- Solve problems 1, 2, 5, 13, 17 and 18 on pages 74-76, problems 1, 5a, 5b, 5c-g, 9, 15 and 16 on pages 84-86 and problems 1, 2, 3a and 3b on pages 96-97, but submit only your solutions of the underlined problems. This assignment is due at the tutorials on Thursday November 9.
- Just for fun. Decide if the vectors and are linearly dependent.