|
|
| (One intermediate revision by the same user not shown) |
| Line 1: |
Line 1: |
|
{{AKT-09/Navigation}} |
|
{{AKT-09/Navigation}} |
|
{{In Preparation}} |
|
|
|
|
|
|
'''Solve the following problems''' and submit them in class by November 24, 2009: |
|
'''Solve the following problems''' and submit them in class by December 1, 2009: |
|
|
|
|
|
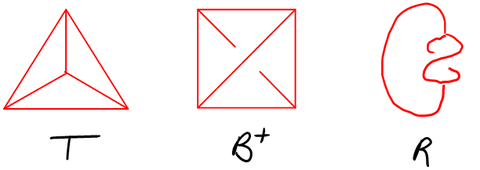
'''Problem 1''' With <math>T</math>, <math>B^+</math> and <math>R</math> as below, write <math>B^+</math> as a composition of <math>T</math> and two <math>R</math>'s, using he basic TG operations <math>d_e</math>, <math>u_e</math>, and <math>\#</math>. |
|
'''Problem 1''' With <math>T</math>, <math>B^+</math> and <math>R</math> as below, write <math>B^+</math> as a composition of <math>T</math> and two <math>R</math>'s, using he basic TG operations <math>d_e</math>, <math>u_e</math>, and <math>\#</math>. |
|
|
|
|
|
⚫ |
<center>[[Image: AKT- 09- TBR. png|480px]]</center> |
| ⚫ |
'''Problem 2''' Show that the "topological boundary" operator <math>\partial_T</math> and the "crossing change" operator <math>x_T</math> of the class of November 5 are compositions of the basic TG operations <math>d_e</math>, <math>u_e</math>, and <math>\#</math> (you are also allowed to use "nullary" operations, otherwise known as "constants"). |
|
|
|
|
|
|
⚫ |
'''Problem 2''' Show that the "topological boundary" operator <math>\partial_T</math> and the "crossing change" operator <math>x_T</math> of the class of November 5 are compositions of the basic TG operations <math>d_e</math>, <math>u_e</math>, and <math>\#</math> (you are also allowed to use "nullary" operations, otherwise known as "constants"). |
| ⚫ |
'''Problem 3''' Write the third Reidemeister move R3 as a relation on <math>Z(B_+)</math> , where <math>B_+</math> is given by the picture below: |
|
|
|
|
|
|
⚫ |
'''Problem 3''' Write the third Reidemeister move R3 as a relation on <math>Z(B_+)</math> . |
| ⚫ |
<center>[[Image: 06- 1350- BPlus. svg]]</center> |
|
Latest revision as of 18:36, 23 November 2009
| #
|
Week of...
|
Videos, Notes, and Links
|
| 1
|
Sep 7
|
About This Class
 090910-1: 3-colourings, Reidemeister's theorem, invariance, the Kauffman bracket. 090910-1: 3-colourings, Reidemeister's theorem, invariance, the Kauffman bracket.
 090910-2: R23 invariance of the bracket, R1, the writhe, the Jones polynomial, programming the Jones polynomial. 090910-2: R23 invariance of the bracket, R1, the writhe, the Jones polynomial, programming the Jones polynomial.
Tricolourability
|
| 2
|
Sep 14
|
 090915: More on Jones, some pathologies and more on Reidemeister, our overall agenda. 090915: More on Jones, some pathologies and more on Reidemeister, our overall agenda.
 090917-1: The definition of finite type, weight systems, Jones is a finite type series. 090917-1: The definition of finite type, weight systems, Jones is a finite type series.
 090917-2: The skein relation for Jones; HOMFLY-PT and Conway; the weight system of Jones. 090917-2: The skein relation for Jones; HOMFLY-PT and Conway; the weight system of Jones.
|
| 3
|
Sep 21
|
 090922: FI, 4T, HOMFLY and FI and 4T, statement of the Fundamental Theorem, framed knots. 090922: FI, 4T, HOMFLY and FI and 4T, statement of the Fundamental Theorem, framed knots.
 090924-1: Some dimensions of [math]\displaystyle{ {\mathcal A}_n }[/math], [math]\displaystyle{ {\mathcal A} }[/math] is a commutative algebra, [math]\displaystyle{ {\mathcal A}(\bigcirc)\equiv{\mathcal A}(\uparrow) }[/math]. 090924-1: Some dimensions of [math]\displaystyle{ {\mathcal A}_n }[/math], [math]\displaystyle{ {\mathcal A} }[/math] is a commutative algebra, [math]\displaystyle{ {\mathcal A}(\bigcirc)\equiv{\mathcal A}(\uparrow) }[/math].
Class Photo
 090924-2: [math]\displaystyle{ {\mathcal A} }[/math] is a co-commutative algebra, the relation with products of invariants, [math]\displaystyle{ {\mathcal A} }[/math] is a bi-algebra. 090924-2: [math]\displaystyle{ {\mathcal A} }[/math] is a co-commutative algebra, the relation with products of invariants, [math]\displaystyle{ {\mathcal A} }[/math] is a bi-algebra.
|
| 4
|
Sep 28
|
Homework Assignment 1
Homework Assignment 1 Solutions
 090929: The Milnor-Moore theorem, primitives, the map [math]\displaystyle{ {\mathcal A}^r\to{\mathcal A} }[/math]. 090929: The Milnor-Moore theorem, primitives, the map [math]\displaystyle{ {\mathcal A}^r\to{\mathcal A} }[/math].
 091001-1: Jacobi diagrams, AS, IHX, STU, and the equivalence of all that with 4T. 091001-1: Jacobi diagrams, AS, IHX, STU, and the equivalence of all that with 4T.
 091001-2: The very basics on Lie algebras. 091001-2: The very basics on Lie algebras.
|
| 5
|
Oct 5
|
 091006: Lie algebraic weight systems, [math]\displaystyle{ gl_N }[/math]. 091006: Lie algebraic weight systems, [math]\displaystyle{ gl_N }[/math].
 091008-1: More on [math]\displaystyle{ gl_N }[/math], Lie algebras and the four colour theorem. 091008-1: More on [math]\displaystyle{ gl_N }[/math], Lie algebras and the four colour theorem.
 091008-2: The "abstract tenssor" approach to weight systems, [math]\displaystyle{ {\mathcal U}({\mathfrak g}) }[/math] and PBW, the map [math]\displaystyle{ {\mathcal T}_{\mathfrak g} }[/math]. 091008-2: The "abstract tenssor" approach to weight systems, [math]\displaystyle{ {\mathcal U}({\mathfrak g}) }[/math] and PBW, the map [math]\displaystyle{ {\mathcal T}_{\mathfrak g} }[/math].
|
| 6
|
Oct 12
|
 091013: Algebraic properties of [math]\displaystyle{ {\mathcal U}({\mathfrak g}) }[/math] vs. algebraic properties of [math]\displaystyle{ {\mathcal A} }[/math]. 091013: Algebraic properties of [math]\displaystyle{ {\mathcal U}({\mathfrak g}) }[/math] vs. algebraic properties of [math]\displaystyle{ {\mathcal A} }[/math].
Thursday's class canceled.
|
| 7
|
Oct 19
|
 091020: Universal finite type invariants, filtered and graded spaces, expansions. 091020: Universal finite type invariants, filtered and graded spaces, expansions.
Homework Assignment 2
The Stonehenge Story
 091022-1: The Stonehenge Story to IHX and STU. 091022-1: The Stonehenge Story to IHX and STU.
 091022-2: The Stonhenge Story: anomalies, framings, relation with physics. 091022-2: The Stonhenge Story: anomalies, framings, relation with physics.
|
| 8
|
Oct 26
|
 091027: Knotted trivalent graphs and their chord diagrams. 091027: Knotted trivalent graphs and their chord diagrams.
 091029-1: Zsuzsi Dancso on the Kontsevich Integral (1). 091029-1: Zsuzsi Dancso on the Kontsevich Integral (1).
 091029-2: Zsuzsi Dancso on the Kontsevich Integral (2). 091029-2: Zsuzsi Dancso on the Kontsevich Integral (2).
|
| 9
|
Nov 2
|
 091103: The details of [math]\displaystyle{ {\mathcal A}^{TG} }[/math]. 091103: The details of [math]\displaystyle{ {\mathcal A}^{TG} }[/math].
 091105-1: Three basic problems: genus, unknotting numbers, ribbon knots. 091105-1: Three basic problems: genus, unknotting numbers, ribbon knots.
 091105-2: The three basic problems and algebraic knot theory. 091105-2: The three basic problems and algebraic knot theory.
|
| 10
|
Nov 9
|
 091110: Tangles and planar algebras, shielding and the generators of KTG. 091110: Tangles and planar algebras, shielding and the generators of KTG.
Homework Assignment 3
No Thursday class.
|
| 11
|
Nov 16
|
Local Khovanov Homology
 091119-1: Local Khovanov homology, I. 091119-1: Local Khovanov homology, I.
 091119-2: Local Khovanov homology, II. 091119-2: Local Khovanov homology, II.
|
| 12
|
Nov 23
|
 091124: Emulation of one structure inside another, deriving the pentagon. 091124: Emulation of one structure inside another, deriving the pentagon.
 091126-1: Peter Lee on braided monoidal categories, I. 091126-1: Peter Lee on braided monoidal categories, I.
 091126-2: Peter Lee on braided monoidal categories, II. 091126-2: Peter Lee on braided monoidal categories, II.
|
| 13
|
Nov 30
|
 091201: The relations in KTG. 091201: The relations in KTG.
 091203-1: The Existence of the Exponential Function. 091203-1: The Existence of the Exponential Function.
 091203-2: The Final Exam, Dror's failures. 091203-2: The Final Exam, Dror's failures.
|
| F
|
Dec 7
|
The Final Exam on Thu Dec 10, 9-11, Bahen 6183.
|
| Register of Good Deeds / To Do List
|

Add your name / see who's in!
|

|
|
Solve the following problems and submit them in class by December 1, 2009:
Problem 1 With [math]\displaystyle{ T }[/math], [math]\displaystyle{ B^+ }[/math] and [math]\displaystyle{ R }[/math] as below, write [math]\displaystyle{ B^+ }[/math] as a composition of [math]\displaystyle{ T }[/math] and two [math]\displaystyle{ R }[/math]'s, using he basic TG operations [math]\displaystyle{ d_e }[/math], [math]\displaystyle{ u_e }[/math], and [math]\displaystyle{ \# }[/math].
Problem 2 Show that the "topological boundary" operator [math]\displaystyle{ \partial_T }[/math] and the "crossing change" operator [math]\displaystyle{ x_T }[/math] of the class of November 5 are compositions of the basic TG operations [math]\displaystyle{ d_e }[/math], [math]\displaystyle{ u_e }[/math], and [math]\displaystyle{ \# }[/math] (you are also allowed to use "nullary" operations, otherwise known as "constants").
Problem 3 Write the third Reidemeister move R3 as a relation on [math]\displaystyle{ Z(B_+) }[/math].


