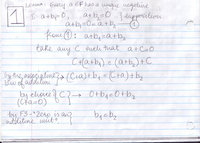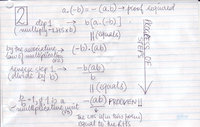06-240/Classnotes For Tuesday, September 12: Difference between revisions
From Drorbn
Jump to navigationJump to search
m (changed file name) |
No edit summary |
||
| (4 intermediate revisions by 3 users not shown) | |||
| Line 6: | Line 6: | ||
* PDF notes by [[User:Alla]]: [[Media:MAT_Lect001.pdf|Week 1 Lecture 1 notes]] |
* PDF notes by [[User:Alla]]: [[Media:MAT_Lect001.pdf|Week 1 Lecture 1 notes]] |
||
* Below are a couple of lemmata critical to the derivation we did in class - the Professor left this little work to the students: |
* Below are a couple of lemmata critical to the derivation we did in class - the Professor left this little work to the students: |
||
::[[Image:Edit1.jpg|200px]] [[Image:Edit2.jpg|200px]] |
|||
** [[06-240: Edit2.jpg]] |
|||
=Notes= |
=Notes= |
||
==The Real Numbers== |
==The Real Numbers== |
||
The Real Numbers are a set (denoted by <math>\mathbb{R}</math>) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true: |
The Real Numbers are a set (denoted by <math>\mathbb{R}</math>) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true: |
||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
This takes way too long. It is probably more practical to type the notes in Word and upload it onto the site, if we want a typesetted version of the notes. |
|||
| ⚫ | |||
| ⚫ | |||
| ⚫ | |||
This is incomplete. |
|||
Latest revision as of 17:13, 11 July 2007
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||
- PDF notes by User:Harbansb: September 12 Notes.
- If I have made an error in my notes, or you would like the editable OpenOffice file, feel free to e-mail me at harbansb@msn.com.
- September 12 Notes for re-uploading, please email at jeff.matskin@utoronto.ca
- PDF notes by User:Alla: Week 1 Lecture 1 notes
- Below are a couple of lemmata critical to the derivation we did in class - the Professor left this little work to the students:
Notes
The Real Numbers
The Real Numbers are a set (denoted by ) along with two binary operations: + (plus) and · (times) and two special elements: 0 (zero) and 1 (one), such that the following laws hold true:
: we have and (The Commutative Laws)
: we have and (The Associative Laws)
: is an additive unit and is a multiplicative unit (The Existence of Units/Identities)
:
This is incomplete.