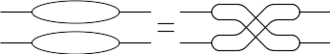The Envelope of The Alexander Polynomial: Difference between revisions
No edit summary |
|||
| Line 24: | Line 24: | ||
{{Equation*|<math>\frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}C(e^{\hbar/2}-e^{-\hbar/2}) = \frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}A(e^\hbar)</math>}} |
{{Equation*|<math>\frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}C(e^{\hbar/2}-e^{-\hbar/2}) = \frac{\hbar}{e^{\hbar/2}-e^{-\hbar/2}}A(e^\hbar)</math>}} |
||
is a canonical Vassiliev power series. Let d denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that <math>W_C(d^{2n})=(-2\hbar^2)^n</math> (in shorter and less precise form, <math>\hbar=W_C(id/\sqrt2)</math>), where <math>W_C</math> is the weight system of the Alexander-Conway polynomial: |
is a canonical Vassiliev power series. Let <math>d</math> denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that <math>W_C(d^{2n})=(-2\hbar^2)^n</math> (in shorter and less precise form, <math>\hbar=W_C(id/\sqrt2)</math>), where <math>W_C</math> is the weight system of the Alexander-Conway polynomial: |
||
'''Theorem.''' Let <math>K</math> be a knot and let <math>Z(K)</math> be the Kontsevich integral of <math>K</math>. Then within the envelope of the Alexander-Conway polynomial, |
'''Theorem.''' Let <math>K</math> be a knot and let <math>Z(K)</math> be the Kontsevich integral of <math>K</math>. Then within the envelope of the Alexander-Conway polynomial, |
||
Latest revision as of 08:13, 1 May 2007
|
The information below is preliminary and cannot be trusted! (v)
The Internal Kernel of the Alexander Polynomial
All that there is here comes from 06-1350/Class Notes for Tuesday October 24. Many further relevant facts are in arXiv:q-alg/9602014 by José M. Figueroa-O'Farrill, Takashi Kimura, Arkady Vaintrob and in arXiv:math.QA/0204346 by Jens Lieberum.
At the moment I know of just three relations in the internal kernel of the Alexander polynomial: the bubble relation, the H relation and the 4Y relation:
I have good reasons to suspect that there are further relations. But at the moment I don't know what they are, so below we will make do with what we have.
The VS-Algebra Envelope of the Alexander Polynomial
Alexander-Conway, Precisely
Let [math]\displaystyle{ C(z) }[/math] denote the Conway polynomial and [math]\displaystyle{ A(t) }[/math] denote the Alexander polynomial. By [Bar-Natan_Garoufalidis_96] we know that
is a canonical Vassiliev power series. Let [math]\displaystyle{ d }[/math] denote "half a bubble". The following theorem follows easily from the above canonicity statement and the fact that [math]\displaystyle{ W_C(d^{2n})=(-2\hbar^2)^n }[/math] (in shorter and less precise form, [math]\displaystyle{ \hbar=W_C(id/\sqrt2) }[/math]), where [math]\displaystyle{ W_C }[/math] is the weight system of the Alexander-Conway polynomial:
Theorem. Let [math]\displaystyle{ K }[/math] be a knot and let [math]\displaystyle{ Z(K) }[/math] be the Kontsevich integral of [math]\displaystyle{ K }[/math]. Then within the envelope of the Alexander-Conway polynomial,
References
[Bar-Natan_Garoufalidis_96] ^ Dror Bar-Natan and Stavros Garoufalidis, On the Melvin-Morton-Rozansky Conjecture, Inventiones Mathematicae 125 (1996) 103-133.