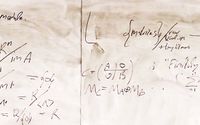|
|
| (3 intermediate revisions by the same user not shown) |
| Line 1: |
Line 1: |
|
{{14-1100/Navigation}} |
|
{{14-1100/Navigation}} |
|
|
|
|
|
'''Here are some handwritten notes about direct sums in a bit more detail:'''
|
|
Here are some handwritten notes about direct sums in a bit more detail: |
|
{| |
|
{| |
|
|[[File:MAT1100 Lec_17, 14-11-10M - direct sums, small p1.pdf]] |
|
|[[File:MAT1100 Lec_17, 14-11-10M - direct sums, small p1.pdf]] |
|
|[[File:MAT1100 Lec 17, 14-11-10M - direct sums, small p2.pdf]] |
|
|[[File:MAT1100 Lec 17, 14-11-10M - direct sums, small p2.pdf]] |
|
⚫ |
|
|
|
Handwritten notes about presentation matrices for finitely generated modules in a bit more detail: |
|
|
''Apologies''! I had found a few mistakes my notes: there are a few places where I'd flipped <math>R^n</math> with X, and other similar errors. |
|
|
|
|
|
Here are some jpg's with corrections, although there may still be other mistakes... |
|
⚫ |
|
|
⚫ |
|[[File: 14-1100 Lec 17, 14-11-10M - module gen by a matrix, small p1. jpg|200px|thumb|left|page 1]] |
|
⚫ |
|[[File: 14-1100 Lec 17, 14-11-10M - module gen by a matrix, small p2. jpg|200px|thumb|left|page 2]] |
|
|
|} |
|
|
{| |
|
|
|[[File: 14-1100 Lec 17, 14-11-10M - module gen by a matrix, small p3.jpg|200px|thumb|left|page 3]] |
|
|} |
|
|} |
|
|
|
|
| Line 53: |
Line 64: |
|
{| |
|
{| |
|
|[[File:14-1100 Lec 17 page 5.JPG|200px|thumb|left|Lec 15 page 5]] |
|
|[[File:14-1100 Lec 17 page 5.JPG|200px|thumb|left|Lec 15 page 5]] |
| ⚫ |
|
|
|
|
|
|
'''Here are some handwritten notes about modules generated by a matrix in a bit more detail:''' |
|
| ⚫ |
|
|
| ⚫ |
|[[File:14-1100 Lec 17, 14-11-10M - module generated by a matrix, small p1. pdf]] |
|
| ⚫ |
|[[File:14-1100 Lec 17, 14-11-10M - module generated by a matrix, small p2. pdf]] |
|
|
|} |
|
|} |
Welcome to Math 1100!
(additions to this web site no longer count towards good deed points)
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 8
|
About This Class; Monday - Non Commutative Gaussian Elimination; Thursday - the category of groups, automorphisms and conjugations, images and kernels.
|
| 2
|
Sep 15
|
Monday - coset spaces, isomorphism theorems; Thursday - simple groups, Jordan-Holder decomposition series.
|
| 3
|
Sep 22
|
Monday - alternating groups, group actions, The Simplicity of the Alternating Groups, HW1, HW 1 Solutions, Class Photo; Thursday - group actions, Orbit-Stabilizer Thm, Class Equation.
|
| 4
|
Sep 29
|
Monday - Cauchy's Thm, Sylow 1; Thursday - Sylow 2.
|
| 5
|
Oct 6
|
Monday - Sylow 3, semi-direct products, braids; HW2; HW 2 Solutions; Thursday - braids, groups of order 12, Braids
|
| 6
|
Oct 13
|
No class Monday (Thanksgiving); Thursday - groups of order 12 cont'd.
|
| 7
|
Oct 20
|
Term Test; Term Test Solutions on Monday, HW3; HW 3 Solutions; Thursday - solvable groups, rings: defn's & examples.
|
| 8
|
Oct 27
|
Monday - functors, Cayley-Hamilton Thm, ideals, iso thm 1; Thursday - iso thms 2-4, integral domains, maximal ideals, One Theorem, Three Corollaries, Five Weeks
|
| 9
|
Nov 3
|
Monday - prime ideals, primes & irreducibles, UFD's, Euc.Domain PID, Thursday - Noetherian rings, PIDUFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions
|
| 10
|
Nov 10
|
Monday - R is a PID iff R has a D-H norm, R-modules, direct sums, every f.g. module is given by a presentation matrix, Thursday - row & column reductions plus, existence part of Thm 1 in 1t3c5w handout.
|
| 11
|
Nov 17
|
Monday-Tuesday is UofT's Fall Break, HW5, Thursday - 1t3c5w handout cont'd, JCF Tricks & Programs handout
|
| 12
|
Nov 24
|
Monday - JCF Tricks & Programs cont'd, tensor products, Thursday - tensor products cont'd
|
| 13
|
Dec 1
|
End-of-Course Schedule; Monday - tensor products finale, extension/reduction of scalars, uniqueness part of Thm 1 in 1t3c5w, localization & fields of fractions; Wednesday is a "makeup Monday"!; Notes for Studying for the Final Exam Glossary of terms
|
| F
|
Dec 15
|
The Final Exam
|
| Register of Good Deeds
|
Add your name / see who's in!
|
See Non Commutative Gaussian Elimination
|
|
Here are some handwritten notes about direct sums in a bit more detail:
Handwritten notes about presentation matrices for finitely generated modules in a bit more detail:
Apologies! I had found a few mistakes my notes: there are a few places where I'd flipped 
with X, and other similar errors.
Here are some jpg's with corrections, although there may still be other mistakes...
Here are some handwritten notes:
