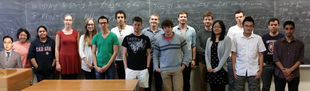14-1100/End-of-Course Schedule

DBN: Classes: 2014-15: 14-1100/Navigation Welcome to Math 1100! (additions to this web site no longer count towards good deed points) # Week of... Notes and Links 1 Sep 8 About This Class; Monday - Non Commutative Gaussian Elimination; Thursday - the category of groups, automorphisms and conjugations, images and kernels. 2 Sep 15 Monday - coset spaces, isomorphism theorems; Thursday - simple groups, Jordan-Holder decomposition series. 3 Sep 22 Monday - alternating groups, group actions, The Simplicity of the Alternating Groups, HW1, HW 1 Solutions, Class Photo; Thursday - group actions, Orbit-Stabilizer Thm, Class Equation. 4 Sep 29 Monday - Cauchy's Thm, Sylow 1; Thursday - Sylow 2. 5 Oct 6 Monday - Sylow 3, semi-direct products, braids; HW2; HW 2 Solutions; Thursday - braids, groups of order 12, Braids 6 Oct 13 No class Monday (Thanksgiving); Thursday - groups of order 12 cont'd. 7 Oct 20 Term Test; Term Test Solutions on Monday, HW3; HW 3 Solutions; Thursday - solvable groups, rings: defn's & examples. 8 Oct 27 Monday - functors, Cayley-Hamilton Thm, ideals, iso thm 1; Thursday - iso thms 2-4, integral domains, maximal ideals, One Theorem, Three Corollaries, Five Weeks 9 Nov 3 Monday - prime ideals, primes & irreducibles, UFD's, Euc.Domain$\Rightarrow$PID, Thursday - Noetherian rings, PID$\Rightarrow$UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions 10 Nov 10 Monday - R is a PID iff R has a D-H norm, R-modules, direct sums, every f.g. module is given by a presentation matrix, Thursday - row & column reductions plus, existence part of Thm 1 in 1t3c5w handout. 11 Nov 17 Monday-Tuesday is UofT's Fall Break, HW5, Thursday - 1t3c5w handout cont'd, JCF Tricks & Programs handout 12 Nov 24 Monday - JCF Tricks & Programs cont'd, tensor products, Thursday - tensor products cont'd 13 Dec 1 End-of-Course Schedule; Monday - tensor products finale, extension/reduction of scalars, uniqueness part of Thm 1 in 1t3c5w, localization & fields of fractions; Wednesday is a "makeup Monday"!; Notes for Studying for the Final Exam Glossary of terms F Dec 15 The Final Exam Register of Good Deeds Add your name / see who's in! See Non Commutative Gaussian Elimination

Here's a tentative activity schedule for the last few days of our class:

• Wednesday December 3, 13PM: Our last class. Note the unusual time - that Wednesday is a "UofT Monday". HW5 is due!

• Wednesday December 3, 3PM-4PM: Office hour.

• Thursday December 4, 10AM-12PM: Riddles session with Dror at Bahen 6183. Not a part of this class! Not mandatory in any way! Also with the students of 14-240.

• Sunday December 14, noon: At 24 hours before the final, edits to this class' web site no longer count for good deed points.

• Sunday December 14, 2-5PM: Pre-final office hours.

• Monday December 15, 10-11AM: Pre-final office hour.

• Monday December 15, 12-3PM: Our final exam at Bahen 6183.

Warning. Last minute changes are possible! Check here before you go.