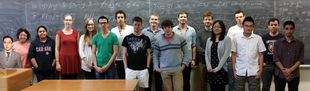Welcome to Math 1100!
(additions to this web site no longer count towards good deed points)
|
| #
|
Week of...
|
Notes and Links
|
| 1
|
Sep 8
|
About This Class; Monday - Non Commutative Gaussian Elimination; Thursday - the category of groups, automorphisms and conjugations, images and kernels.
|
| 2
|
Sep 15
|
Monday - coset spaces, isomorphism theorems; Thursday - simple groups, Jordan-Holder decomposition series.
|
| 3
|
Sep 22
|
Monday - alternating groups, group actions, The Simplicity of the Alternating Groups, HW1, HW 1 Solutions, Class Photo; Thursday - group actions, Orbit-Stabilizer Thm, Class Equation.
|
| 4
|
Sep 29
|
Monday - Cauchy's Thm, Sylow 1; Thursday - Sylow 2.
|
| 5
|
Oct 6
|
Monday - Sylow 3, semi-direct products, braids; HW2; HW 2 Solutions; Thursday - braids, groups of order 12, Braids
|
| 6
|
Oct 13
|
No class Monday (Thanksgiving); Thursday - groups of order 12 cont'd.
|
| 7
|
Oct 20
|
Term Test; Term Test Solutions on Monday, HW3; HW 3 Solutions; Thursday - solvable groups, rings: defn's & examples.
|
| 8
|
Oct 27
|
Monday - functors, Cayley-Hamilton Thm, ideals, iso thm 1; Thursday - iso thms 2-4, integral domains, maximal ideals, One Theorem, Three Corollaries, Five Weeks
|
| 9
|
Nov 3
|
Monday - prime ideals, primes & irreducibles, UFD's, Euc.Domain PID, Thursday - Noetherian rings, PID PID, Thursday - Noetherian rings, PID UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions UFD, Euclidean Algorithm, modules: defn & examples, HW4, HW 4 Solutions
|
| 10
|
Nov 10
|
Monday - R is a PID iff R has a D-H norm, R-modules, direct sums, every f.g. module is given by a presentation matrix, Thursday - row & column reductions plus, existence part of Thm 1 in 1t3c5w handout.
|
| 11
|
Nov 17
|
Monday-Tuesday is UofT's Fall Break, HW5, Thursday - 1t3c5w handout cont'd, JCF Tricks & Programs handout
|
| 12
|
Nov 24
|
Monday - JCF Tricks & Programs cont'd, tensor products, Thursday - tensor products cont'd
|
| 13
|
Dec 1
|
End-of-Course Schedule; Monday - tensor products finale, extension/reduction of scalars, uniqueness part of Thm 1 in 1t3c5w, localization & fields of fractions; Wednesday is a "makeup Monday"!; Notes for Studying for the Final Exam Glossary of terms
|
| F
|
Dec 15
|
The Final Exam
|
| Register of Good Deeds
|
Add your name / see who's in!
|

See Non Commutative Gaussian Elimination
|
|
Bad news. This assignment is due at class time on Thursday, October 16, 2010.
Good news. It will be marked by the following day, Friday October 17, and be available for pickup at my office between 2-4PM, providing you timely feedback for the term test on the following Monday.
Solve the following problems
(but submit only your solutions of problems 2, 3, 4, 8, 9, and 11).
Problem 1. (Selick)
- What it the least integer
 for which the symmetric group
for which the symmetric group  contains an element of order 18?
contains an element of order 18?
- What is the maximal order of an element in
 ? (That is, of a shuffling of the red cards within a deck of cards?)
? (That is, of a shuffling of the red cards within a deck of cards?)
Problem 2. (Selick) Let  be a subgroup of index 2 in a group
be a subgroup of index 2 in a group  . Show that
. Show that  is normal in
is normal in  .
.
Problem 3. Let  be a permutation whose cycle decomposition consists of one 5-cycle, two 3-cycles, and one 2-cycle. What is the order of the centralizer
be a permutation whose cycle decomposition consists of one 5-cycle, two 3-cycles, and one 2-cycle. What is the order of the centralizer  of
of  ?
?
Problem 4. (Selick) Let  be a group of odd order. Show that
be a group of odd order. Show that  is not conjugate to
is not conjugate to  unless
unless  .
.
Problem 5. (Dummit and Foote) Show that if  is cyclic then
is cyclic then  is Abelian.
is Abelian.
Problem 6. (Lang) Prove that if the group of automorphisms of a group  is cyclic, then
is cyclic, then  is Abelian.
is Abelian.
Problem 7. (Lang)
- Let
 be a group and let
be a group and let  be a subgroup of finite index. Prove that there is a normal subgroup
be a subgroup of finite index. Prove that there is a normal subgroup  of
of  , contained in
, contained in  , so that
, so that  is also finite. (Hint: Let
is also finite. (Hint: Let  and find a morphism
and find a morphism  whose kernel is contained in
whose kernel is contained in  .)
.)
- Let
 be a group and
be a group and  and
and  be subgroups of
be subgroups of  . Suppose
. Suppose  and
and  . Show that
. Show that 
Problem 8. (Selick) Show that any group of order 56 has a normal Sylow- subgroup, for some prime
subgroup, for some prime  dividing 56.
dividing 56.
Problem 9. (Qualifying exam, May 1997) Let  act on
act on  by permuting the factors, and let
by permuting the factors, and let  be the semi-direct product of
be the semi-direct product of  and
and  .
.
- What is the order of
 ?
?
- How many Sylow-5 subgroups does
 have? Write down one of them.
have? Write down one of them.
Problem 10. (Selick) Show that the group  of unit quaternions (
of unit quaternions ( , subject to
, subject to  and
and  ) is not a semi-direct product of two of its proper subgroups.
) is not a semi-direct product of two of its proper subgroups.
Problem 11. (Qualifying exam, September 2008) Let  be a finite group and
be a finite group and  be a prime. Show that if
be a prime. Show that if  is a
is a  -subgroup of
-subgroup of  , then
, then  is congruent to
is congruent to  mod
mod  . You may wish to study the action of
. You may wish to study the action of  on
on  by multiplication on the left.
by multiplication on the left.