06-1350/Class Notes for Thursday November 16

#	Week of...	Links
1	Sep 11	About, Tue, Thu
2	Sep 18	Tue, Kurlin(P), Thu
3	Sep 25	Tue, Photo, Thu
4	Oct 2	HW1, Tue, Thu
5	Oct 9	Tue(P), Thu(P)
6	Oct 16	HW2, Tue(P), Thu(P)
7	Oct 23	Tue(P), Thu
8	Oct 30	HW3, Tue, Thu
9	Nov 6	Tue ( $ν$ ), Thu
10	Nov 13	Tue, Thu
11	Nov 20	HW4(P), Thu
12	Nov 27	Thu
13	Dec 4	Syzygies in Asymptote, Final
	Jan 8	Grades
Note. (P) means "contains a problem that Dror cares about".
Add your name / see who's in!
On to 07-1352

Today's Agenda

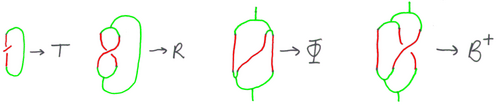
Sweeping clean a tree and ${\mathcal A}(\Gamma)\equiv{\mathcal A}(\uparrow_{b_1(\Gamma)})$ .

${\mathcal A}(\uparrow_n)$ is a VS-algebra (see more at VS, TS and TG Algebras).

In the coordinates above, write the TRΦB relations in various algebraic notations.
- R4: $(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star\Phi=(1123)^\star\Phi\cdot(1233)^\star B$ or $(B 1 a B 2 a Φ 1 a; B 1 b B 2 b; B 1 c B 2 a Φ 1 b; B 2 c Φ 1 c) = (Φ 2 a B 3 a;Φ 2 a B 3 b;Φ 2 b B 3 c;Φ 2 c B 3 c)$ .
- R3: $(1230)^\star B\cdot(1213)^\star B\cdot(1023)^\star B = (1123)^\star B\cdot(1203)^\star B\cdot(1231)^\star B$ or $(B 1 a B 2 a B 3 a; B 1 b B 2 b; B 1 c B 2 a B 3 b; B 2 c B 3 c) = (B 4 a B 5 a B 6 a; B 4 a B 5 b B 6 b; B 4 b B 6 c; B 4 c B 5 c B 6 a)$ .
- R2: $(123)^\star B^\pm\cdot(132)^\star B^\mp=1_3$ or $(B^\pm_{1a}B^\mp_{2a}; B^\pm_{2b}B^\mp_{3c}; B^\pm_{1c}B^\mp_{2b}) = (1;1;1)$ .
- R1: $(B^\pm_a; B^\pm_bB^\pm_c)=(1;T^{\pm 2})$ .
But for now, skip the writing of the following relations:
- Symmetry of $Φ$ and of $B^{\pm}$ .
- $u$ , $d$ and $\#$
- Idempotence for $T$ , $R$ , $Φ$ and $B^{\pm}$ .
- $B^{\pm}$ in terms of $Φ$ and $R$ and $R$ in terms of $T$ .