Survey of Finite Type Invariants
This is an overview article on finite type invariants. It is the Wiki form of the article Finite Type Invariants by Dror Bar-Natan. It was printed at the Encyclopedia of Mathematical Physics, eds. J.-P. Francoise, G.L. Naber and Tsou S.T., Oxford: Elsevier, 2006 (ISBN 0-12-512660-3), volume 2 page 340.
This work was partially supported by NSERC grant RGPIN 262178.
Editing? Go to the #Done Line.
Introduction
Knots belong to sailors and climbers and upon further reflection, perhaps also to geometers, topologists or combinatorialists. Surprisingly, throughout the 1980s it became apparent that knots are also closely related to several other branches of mathematics in general and mathematical physics in particular. Many of these connections (though not all!) factor through the notion of "finite type invariants" (aka "Vassiliev" or "Goussarov-Vassiliev" invariants) ([Goussarov_91], [Goussarov_93], [Vassiliev_90], [Vassiliev_92], [Birman_Lin_93], [Kontsevich_93], [Bar-Natan_95]).
Let be an arbitrary invariant of oriented knots in oriented space with values in some Abelian group . Extend to be an invariant of -singular knots, knots that may have a single singularity that locally looks like a double point ![]() , using the formula
, using the formula
where
|
(eq:DoublePoint) |
Further extend to the set of -singular knots (knots with double points) by repeatedly using (eq:DoublePoint).
Definition. We say that is of type if its extension to -singular knots vanishes identically. We say that is of finite type if it is of type for some .
Repeated differences are similar to repeated derivatives and hence it is fair to think of the definition of as repeated differentiation. With this in mind, the above definition imitates the definition of polynomials of degree . Hence finite type invariants can be thought of as "polynomials" on the space of knots.
As we shall see below, finite type invariants are plenty and powerful and they carry a rich algebraic structure and are deeply related to Lie algebras (#Basic facts). There are several constructions for a "universal finite type invariant" and those are related to conformal field theory, the Chern-Simons-Witten topological quantum field theory and Drinfel'd's theory of associators and quasi-Hopf algebras (#Proofs of the Fundamental Theorem). Finite type invariants have been studied extensively (#Some further directions) and generalized in several directions (#Beyond knots). But the first question on finite type invariants remains unanswered:
Problem. Honest polynomials are dense in the space of functions. Are finite type invariants dense within the space of all knot invariants? Do they separate knots?
In a similar way one may define finite type invariants of framed knots (and ask the same questions).
Acknowledgement
I wish to thank O. Dasbach and A. Savage for comments and corrections.
Basic facts
Classical knot polynomials
| *Finite type invariants are like polynomials on the space of knots; the standard phrase "knot polynomials" refers to a different thing - knot invariants with polynomial values. |
The first (non trivial!) thing to notice is that there are plenty of finite type invariants and they are at least as powerful as all the standard knot polynomials* combined:
Theorem. ([Bar-Natan_95], [Birman_Lin_93]) Let be the Jones polynomial of a knot (it is a Laurent polynomial in a variable ). Consider the power series expansion . Then each coefficient is a finite type knot invariant. (And thus the Jones polynomial can be reconstructed from finite type information).
A similar theorem holds for the Alexander-Conway, HOMFLY-PT and Kauffman polynomials [Bar-Natan_95], and indeed, for arbitrary Reshetikhin-Turaev invariants ([Reshetikhin_Turaev_90], [Lin_91]). Though it is still unknown if the signature of a knot can be expressed in terms of its finite type invariants.
Chord diagrams and the Fundamental Theorem
The top derivatives of a multi-variable polynomial form a system of constants that determine that polynomial up to polynomials of lower degree. Likewise the th derivative of a type invariant is a constant (for so is blind to 3D topology) and likewise determines up to invariants of lower type. Hence a primary tool in the study of finite type invariants is the study of the "top derivative" , also known as "the weight system of ".
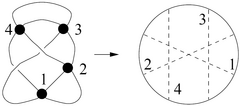
Blind to 3D topology, only sees the combinatorics of the circle that parametrizes an -singular knot. On this circle there are pairs of points that are pairwise identified in the image; standardly one indicates those by drawing a circle with chords marked (an "-chord diagram") as on the right.
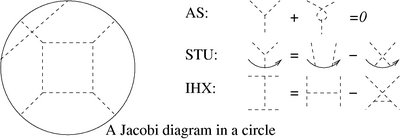
Definition. Let denote the space of all formal linear combinations with rational coefficients of -chord diagrams. Let be the quotient of by all and relations as drawn below (full details in e.g. [Bar-Natan_95]), and let be the graded completion of . Let , and be the same as , and but without imposing the relations.
: 
|
: |
Theorem. (The Fundamental Theorem)
- (Easy part, [Vassiliev_90], [Goussarov_91], [Birman_Lin_93]). If is a rational valued type invariant then defines a linear functional on . If in addition , then is of type .
- (Hard part, [Kontsevich_93] and (#Proofs of the Fundamental Theorem)). For any linear functional on there is a rational valued type invariant so that .
Thus to a large extent the study of finite type invariants is reduced to the finite (though super exponential in ) algebraic study of . A similar theorem reduces the study of finite type invariants of framed knots to the study of .
The structure of
Knots can be multiplied (the "connected sum" operation) and knot invariants can be multiplied. This structure interacts well with finite type invariants and induces the following structure on and :
Theorem. ([Kontsevich_93], [Bar-Natan_95], [Willerton_96], [Chmutov_Duzhin_Lando_94]) and are commutative and cocommutative graded bialgebras (i.e., each carries a commutative product and a compatible cocommutative coproduct). Thus both and are graded polynomial algebras over their spaces of primitives, and .
Framed knots differ from knots only by a single integer parameter (the "self linking", itself a type invariant). Thus and are also closely related.
Theorem. [Bar-Natan_95] , where is the unique -chord diagram ![]() .
.
Bounds and computational results
The following table (taken from [Bar-Natan_95] and [Kneissler_97]) shows the number of type invariants of knots and framed knots modulo type invariants ( and ) and the number of multiplicative generators of the algebra in degree () for . Some further tabulated results are in [Bar-Natan_96].
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 1 | 0 | 1 | 1 | 3 | 4 | 9 | 14 | 27 | 44 | 80 | 132 | 232 | |
| 1 | 1 | 2 | 3 | 6 | 10 | 19 | 33 | 60 | 104 | 184 | 316 | 548 | |
| 0 | 1 | 1 | 1 | 2 | 3 | 5 | 8 | 12 | 18 | 27 | 39 | 55 |
Little is known about these dimensions for large . There is an explicit conjecture in [Broadhurst_97] but no progress has been made in the direction of proving or disproving it. The best asymptotic bounds available are:
Theorem. For large , (for any fixed , see [Dasbach_00], [Kontsevich]) and ([Stoimenow_98], [Zagier_01]).
Jacobi diagrams and the relation with Lie algebras
Much of the richness of finite type invariants stems from their relationship with Lie algebras. The theorem below suggests this relationship on an abstract level, while the following theorem makes that relationship concrete and the theorem after that makes it a bit deeper.
Theorem. [Bar-Natan_95] The algebra is isomorphic to the algebra generated by "Jacobi diagrams in a circle" (chord diagrams that are also allowed to have oriented internal trivalent vertices) modulo the , and relations. See the figure on the right.
Thinking of trivalent vertices as graphical analogs of the Lie bracket, the relation become the anti-commutativity of the bracket, become the equation and becomes the Jacobi identity. This analogy is made concrete within the proof of the following:
Theorem. [Bar-Natan_95] Given a finite dimensional metrized Lie algebra (e.g., any semi-simple Lie algebra) there is a map defined on and taking values in the invariant part of the universal enveloping algebra of . Given also a finite dimensional representation of there is a linear functional .
The last assertion along with The Fundamental Theorem show that associated with any , and there is a weight system and hence a knot invariant. Thus knots are unexpectedly linked with Lie algebras.
Done Line
The hope [Bar-Natan_95] that all finite type invariants arise in this way was dashed by~\Cite{Vogel~97,~99, Lieberum~99}{Vogel:Structures, Vogel:UniversalLieAlgebra, Lieberum:NotComing}. But finite type invariants that do not arise in this way remain rare and not well understood.
The Poincar\'e-Birkhoff-Witt (PBW) theorem of the theory of Lie algebras says that the obvious ``symmetrization map $\chi_\frakg:\calS(\frakg)\to\calU(\frakg)$ from the symmetric algebra $\calS(\frakg)$ of a Lie algebra $\frakg$ to its universal enveloping algebra $\calU(\frakg)$ is a $\frakg$-module isomorphism. The following definition and theorem form a diagrammatic counterpart of this theorem:
\parpic(12mm,13mm)[r]{\raisebox{-14mm}{$
\eps{width=11mm}{BExample}
$}} \begin{definition} Let $\calB$ be the space of formal linear combinations of ``free Jacobi diagrams (Jacobi diagrams as before, but with unmarked univalent ends (``legs) replacing the circle; see an example on the right), modulo the $AS$ and $IHX$ relations of before. Let $\chi:\calB\to\calA$ be the symmetrization map which maps a $k$-legged free Jacobi diagram to the average of the $k!$ ways of planting these legs along a circle. \end{definition}
\parpic(28mm,20mm)[r]{\raisebox{-2mm}{$\xymatrix{
\calB \ar[r]^\chi \ar[d]^{\calT_\frakg} & \calA \ar[d]^{\calT_\frakg} \\
\calS(\frakg) \ar[r]^{\chi_\frakg} & \calU(\frakg)
}$}} \begin{theorem} \label{thm:PBW} (diagrammatic PBW, \Cite{Kontsevich~93, Bar-Natan~95}{Kontsevich:Vassiliev, Bar-Natan:OnVassiliev}) $\chi$ is an isomorphism of vector spaces. Furthermore, fixing a metrized $\frakg$ there is a commutative square as on the right. \end{theorem}
Note that $\calB$ can be graded (by half the number of vertices in a Jacobi diagram) and that $\chi$ respects degrees so it extends to an isomorphism $\chi:\hat\calB\to\hat\calA$ of graded completions.
Proofs of the Fundamental Theorem
\label{sec:Fundamental}
The heart of all known proofs of Theorem~\ref{thm:Fundamental} is always a construction of a ``universal finite type invariant (see below); it is simple to show that the existence of a universal finite type invariant is equivalent to Theorem~\ref{thm:Fundamental}.
\begin{definition} A universal finite type invariant is a map $Z:\{\text{knots}\}\to\hat\calA^r$ whose extension to singular knots satisfies $Z(K)=D+(\text{higher degrees})$ whenever a singular knot $K$ and a chord diagram $D$ are related as in Section~\ref{subsec:ChordDiagrams}. \end{definition}
The Kontsevich Integral
\label{sec:KontsevichIntegral} The first construction of a universal finite type invariant was given by Kontsevich~\Cite{Kontsevich~93}{Kontsevich:Va ssiliev} (see also~\Cite{Bar-Natan~95, Chmutov-Duzhin~01}{Bar-Natan:OnVassiliev, ChmutovD uzhin:KontsevichIntegral}). It is known as ``the Kontsevich Integral and up to a normalization factor it is given by\footnote{
The symbol $\sumint$ means ``sum over all discrete variables and integrate over all continuous variables.
} \[ Z_1(K)=\sum_{m=0}^\infty \frac{1}{(2\pi i)^m}
\hspace{-4mm}
\sumint_{\stackrel{t_1<\ldots<t_m}{P=\{(z_i,z'_i)\}}}
\hspace{-4mm}
(-1)^{\#P_{\downarrow}}D_P
\bigwedge_{i=1}^{m}\frac{dz_i-dz'_i}{z_i-z'_i},
\] where the relationship between the knot $K$, the pairing $P$, the real variables $t_i$, the complex variables $z_i$ and $z'_i$ and the chord diagram $D_P$ is summarized by the figure \[ \eps{width=3in}{DP}. \]
The Kontsevich Integral arises from studying the holonomy of the Knizhnik-Zamolodchikov equation of conformal field theory~\cite{KnizhnikZamolodchikov:CurrentAlgebra}. When evaluating $Z_1$ one encounters multiple $\zeta$-numbers~\Cite{Le-Murakami~95}{LeMurakami:HOMFLY} in a substantial way, and the proof that the end result is rational is quite involved~\Cite{Le-Murakami~96}{LeMurakami:Universal} and relies on deep results about associators and quasitriangular Quasi-Hopf algebras~\cite{Drinfeld:QuasiHopf, Drinfeld:GalQQ}. Employing the same techniques, in~\Cite{Le-Murakami~96}{LeMurakami:Universal} it is also shown that the composition of $W_{\frakg,R}\circ Z_1$ precisely reproduces the Reshetikhin Turaev invariants~\cite{ReshetikhinTuraev:Ribbon}.
Perturbative Chern-Simons-Witten theory and configuration space integrals
\label{sec:CS} Historically the first approach to the construction of a universal finite type invariant was to use perturbation theory with the Chern-Simons-Witten topological quantum field theory; this is also how the relationship with Lie algebras first arose~\Cite{Bar-Natan~91}{Bar-Natan:Thesis}. But taming the integrals involved t urned out to be difficult and working constructions using this approach appeared only a bit later~\Cite{Bott-Taubes~94, Thurston~95, Altschuler-Freidel~97}{BottTaubes:SelfLinking, Thurston:IntegralExpressions, AltschulerFreidel:AllOrders}.
In short, one writes a perturbative expansion for the large $k$ asymptotics of the Chern-Simons-Witten path integral for some metrized Lie algebra $\frakg$ with a Wilson loop in some representation $R$ of $\frakg$, \[
\int_{\frakg\mbox{\scriptsize -connections}}
\hspace{-42pt} \calD A\,
\mbox{\it tr}_R\mbox{\it hol}_K(A)\exp\left[{\scriptstyle
\frac{ik}{4\pi}\int\limits_{\bbR^3}
\mbox{tr}\left(A\wedge dA+\frac{2}{3}A\wedge A\wedge A\right)
}\right].
\] The result is of the form \[
\sum_{\parbox{0.7in}{\centering\scriptsize $D$: Feynman diagram}}
W_{\frakg(D),R}\sumint\calE(D)
\] where $\calE(D)$ is a very messy integral expression and the diagrams $D$ as well as the weights $W_{\frakg(D),R}$ are as in Section~\ref{subsec:Jacobi}. Replacing $W_{\frakg(D),R}$ by simply $D$ in the above formula we get an expression with values in $\hat\calA$: \[ Z_2(K):=\sum_D D\sumint\calE(D)\in\hat\calA. \]
For formal reasons $Z_2(K)$ ought to be a universal finite type invariant, and after much work taming the $\calE(D)$ factors and after multiplying by a further framing-dependent renormalization term $Z^{\text{anomaly}}$, the result is indeed a universal finite type invariant.
Upon further inspection the $\calE(D)$ factors can be reinterpreted as integrals of certain spherical volume forms on certain (compactified) configuration spaces~\Cite{Bott-Taubes~94}{BottTaubes:SelfLinking}. These integrals can be further interpreted as counting certain ``tinker toy constructions built on top of $K$~\Cite{Thurston~95}{Thurston:IntegralExpressions}. The latter viewpoint makes the construction of $Z_2$ visually appealing~\Cite{Bar-Natan~00}{Bar-Natan:AstrologyToTopology}, but there is no satisfactory writeup of this perspective yet.
We note that the precise form of the renormalization term $Z^{\text{anomaly}}$ remains an open problem. An appealing conjecture is that $Z^{\text{anomaly}}=\exp\frac12\isolatedchord$. If this is true then $Z_2=Z_1$ \Cite{Poirier~99}{Poirier:LimitConfigurationSpace}; but the conjecture is only verified up to degree 6 \Cite{Lescop~01}{Lescop:ForLinks} (there's also an unconfirmed verification to all orders~\Cite{Yang~97}{Yang:DegreeTheory}).
The most important open problem about perturbative Chern-Simons-Witten theory is not directly about finite type invariants, but it is nevertheless worthwhile to recall it here:
\begin{problem} Does the perturbative expansion of the Chern-Simons-Witten theory converge (or is asymptotic to) the exact solution due to Witten~\cite{Witten:Jones} and Reshetikhin-Turaev~\cite{ReshetikhinTuraev:Ribbon} when the parameter $k$ converges to infinity? \end{problem}
Associators and trivalent graphs
There is also an entirely algebraic approach for the construction of a universal finite type invariant $Z_3$. The idea is to find some algebraic context within which knot theory is finitely presented --- i.e., presented by finitely many generators subject to finitely many relations. If the algebraic context at hand is compatible with the definitions of finite type invariants and of chord diagrams, one may hope to define $Z_3$ by defining it on the generators in such a way that the relations are satisfied. Thus the problem of defining $Z_3$ is reduced to finding finitely many elements of $\calA$-like spaces which solve certain finitely many equations.
A concrete realization of this idea is in~\Cite{Le-Murakami~96, Bar-Natan~97}{LeMurakami:Universal, Bar-Natan:NAT} (following ideas from~\cite{Drinfeld:QuasiHopf, Drinfeld:GalQQ} on quasitriangular Quasi-Hopf algebras). The relevant ``algebraic context is a category with certain extra operations, and within it, knot theory is generated by just two elements, the braiding $\lrg{\overcrossing}$ and the re-association $\lrg{\Associator}$. Thus to define $Z_3$ it is enough to find $R=Z_3(\lrg{\overcrossing})$ and ``an associator $\Phi=Z_3(\lrg{\Associator})$
which
satisfy certain normalization conditions as well as the pentagon and hexagon equations \[
\Phi^{123}\cdot(1\Delta 1)(\Phi)\cdot\Phi^{234}
=(\Delta 1 1)(\Phi)\cdot
(1 1\Delta)(\Phi),
\] \[
(\Delta 1)(R^{\pm})
= \Phi^{123} (R^{\pm})^{23}(\Phi^{-1})^{132}
(R^{\pm})^{13}\Phi^{312}.
\]
As it turns out the solution for $R$ is easy and nearly canonical. But finding an associator $\Phi$ is a lot harder. There is a closed form integral expression $\Phi^{KZ}$ due to~\cite{Drinfeld:QuasiHopf} but one encounters the same not-too-well-understood multiple $\zeta$ numbers of Section~\ref{sec:KontsevichIntegral}. There is a rather complicated iterative procedure for finding an associator~\cite{Drinfeld:GalQQ, Bar-Natan:Associators}, \Cite{Bar-Natan~97}{Bar-Natan:NAT}. On a computer it had been used to find an associator up to degree $7$. There is also closed form associator that works only with the Lie super-algebra $gl(1|1)$~\Cite{Lieberum~02}{Lieberum:gl11}. But it remains an open problem to find a closed form formula for a rational associator (existence by~\cite{Drinfeld:GalQQ, Bar-Natan:Associators}).
On the positive side we should note that the end result, the invariant $Z_3$, is independent of the choice of $\Phi$ and that $Z_3=Z_1$~\Cite{Le-Murakami~96}{LeMurakami:Universal}.
There is an alternative (more symmetric and intrinsicly 3-dimensional, but less well documented) description of the theory of associators in terms of knotted trivalent graphs~\cite{Bar-NatanThurston:AlgebraicStructures}, \Cite{Thurston~01}{Thurston:Shadow}. There ought to be a perturbative invariant associated with knotted trivalent graphs in the spirit of Section~\ref{sec:CS} and such an invariant should lead to a simple proof that $Z_2=Z_3=Z_1$. But the $\calE(D)$ factors remain untamed in this case.
Step by step integration
\label{subsec:StepByStep} The last approach for proving the Fundamental Theorem is the most natural and historically the first. But here it is last because it is yet to lead to an actual proof. A weight system $W:\calA^r_m\to\bbQ$ is an invariant of $m$-singular knots. We want to show that it is the $m$th derivative of an invariant $V$ of non-singular knots. It is natural to try to integrate $W$ step by step, first finding an invariant $V^{m-1}$ of $(m-1)$-singular knots whose derivative in the sense of~\eqref{eq:doublepoint} is $W$, then an invariant $V^{m-2}$ of $(m-2)$-singular knots whose derivative is $V^{m-1}$, and so on all the way up to an invariant $V^0=V$ whose $m$th derivative will then be $W$. If proven, the following conjecture would imply that such an inductive procedure can be made to work:
\begin{conjecture} \Cite{Hutchings~98}{Hutchings:SingularBraids} If $V^r$ is a once-integrable invariant of $r$-singular knots then it is also twice integrable. That is, if there is an invariant $V^{r-1}$ of $(r-1)$-singular knots whose derivative is $V^r$, then there is an invariant $V^{r-2}$ of $(r-2)$-singular knots whose second derivative is $V^r$. \end{conjecture}
In~\Cite{Hutchings~98}{Hutchings:SingularBraids} Hutchings reduced this conjecture to a certain appealing topological statement and further to a certain combinatorial-algebraic statement about the vanishing of a certain homology group $H^1$ which is probably related to Kontsevich's graph homology complex~\Cite{Kontsevich~94}{Kontsevich:FeynmanDiagrams} (Kontsev ich's $H^0$ is $\calA$, so this is all in the spirit of many deformation theory problems where $H^0$ enumerates infinitesimal deformations and $H^1$ is the obstruction to globalization). Hutchings~\Cite{Hutchings~98}{Hutchings:SingularBraids} was also able to prove t he vanishing of $H^1$ (and hence reprove the Fundamental Theorem) in the simpler case of braids. But no further progress has been made along these lines since~\Cite{Hutchings~98}{Hutchings:SingularBraids}.
Some further directions
\label{sec:FurtherDirections}
We would like to touch on a number of significant further directions in the theory of finite type invariants. We will only say a few words on each of those and refer the reader to the literature for further information.
The original "Vassiliev" perspective
V.A.~Vassiliev came to the study of finite type knot invariants by studying the infinite dimensional space of all immersions of a circle into $\bbR^3$ and the topology of the ``discriminant, the locus of all singular immersions within the latter space~\Cite{Vassiliev~90,~92}{Vassiliev:CohKnot, Vassiliev:Book}. Vassiliev studied the topology of the complement of the discriminant (the space of embeddings) using a certain spectral sequence and found that certain terms in it correspond to finite type invariants. This later got related to the Goodwillie calculus and back to the configuration spaces of Section~\ref{sec:CS}. See~\Cite{Volic~04}{Volic:TaylorTowers}.
Interdependent modifications
The standard definition of finite type invariants is based on modifying a knot by replacing over (or under) crossings with under (or over) crossings. In~\Cite{Goussarov~98}{Goussarov:Modifications} Goussarov generalized this by allowing arbitrary modifications done to a knot --- just take any segment of the knot and move it anywhere else in space. The resulting new ``finite type theory turns out to be equivalent to the old one though with a factor of $2$ applied to the grading (so an ``old type $m$ invariant is a ``new type $2m$ invariant and vice versa). See also~\Cite{Bar-Natan~01, Conant~03}{Bar-Natan:Bracelets, Conant:OnGoussarov}.
-equivalence, commutators and claspers
While little is known about the overall power of finite type invariants, much is known about the power of type $n$ invariants for any given $n$. Goussarov~\Cite{Goussarov~93}{Goussarov:nEquivalence} defined the notion of $n$-equivalence: two knots are said to be ``$n$-equivalent if all their type $n$ invariants are the same. This equivalence relation is well understood both in terms of commutator subgroups of the pure braid group~\Cite{Stanford~98, Ng-Stanford~99}{Stanford:ModuloPureBraids, NgStanford:GusarovGroup} and in terms of Habiro's calculus of surgery over ``claspers~\Cite{Habiro~00}{Habiro:Claspers} (the latter calculus also gives a topological explanation for the appearance of Jacobi diagrams as in Section~\ref{subsec:Jacobi}). In particular, already Goussarov~\Cite{Goussarov~93}{Goussarov:nEquivalence} shows that the set of equivalence classes of knots modulo $n$-equivalence is a finitely generated Abelian group $G_n$ under the operation of connected sum, and the rank of that group is equal to the dimension of the space of type $n$ invariants.
Ng~\Cite{Ng~98}{Ng:Ribbon} has shown that ribbon knots generate an index $2$ subgroup of $G_n$.
Polynomiality and Gauss sums
Goussarov~\Cite{Goussarov~98}{Goussarov:PresentedByGauss} (see also~\Cite{Goussarov-Polyak-Viro~00}{GoussarovPolyakViro:VirtualKnots}) found an intriguing way to compute finite type invariants from a Gauss diagram presentation of a knot, showing in particular that finite type invariants grow as polynomials in the number of crossings $n$ and can be computed in polynomial time in $n$ (though actual computer programs are still missing!).
Gauss diagrams are obtained from knot diagrams in much of the same way as Chord diagrams are obtained from singular knots, except all crossings are counted and not just the double points, and certain over/under and sign information is associated with each crossing/chord so that the knot diagram can be recovered from its Gauss diagram. In the example below, we also dashed a subdiagram of the Gauss diagram equivalent to the chord diagram $\eps{width=7mm}{CD123123}$: \[ \eps{width=2.4in}{GaussDiagram} \]
If $G$ is a Gauss diagram and $D$ is a chord diagram we let $\langle D,G\rangle$ be the number of subdiagrams of $G$ equivalent to $D$, counted with appropriate signs (to be precise, we also need to base the diagrams involved and count subdiagrams that respect the basing).
\begin{theorem} \Cite{Goussarov~98, Goussarov-Polyak-Viro~00}{Goussarov:PresentedByGauss, GoussarovPolyakViro:VirtualKnots} If $V$ is a type $m$ invariant then there are finitely many (based) chord diagrams $D_i$ with at most $m$ chords and rational numbers $\alpha_i$ so that $V(K)=\sum_i\alpha_i\langle D_i,G\rangle$ whenever $G$ is a Gauss diagram representing a knot $K$. \end{theorem}
Computing the Kontsevich Integral
While the Kontsevich Integral $Z_1$ is a cornerstone of the theory of finite type invariants, it has been computed for surprisingly few knots. Even for the unknot the result is non-trivial:
\begin{theorem} \label{thm:Wheels} (``Wheels, \Cite{Bar-Natan-Garoufalidis-Rozansky-Thurston~00, Bar-Natan-Le-Thurston~03}{Bar-NatanGaroufalidisRozanskyThurston:WheelsWheeling, Bar-NatanLeThurston:TwoApplications}) The framed Kontsevich integral of the unknot, $Z_1^F(\bigcirc)$, expressed in terms of diagrams in $\hat\calB$, is given by $\Omega=\exp_\udot \sum_{n=1}^\infty b_{2n}\omega_{2n}$, where the `modified Bernoulli numbers' $b_{2n}$ are defined by the power series expansion $\sum_{n=0}^\infty b_{2n}x^{2n} = \frac{1}{2}\log\frac{\sinh x/2}{x/2}$, the `$2n$-wheel' $\omega_{2n}$ is the free Jacobi diagram made of a $2n$-gon with $2n$ legs (so e.g., $\omega_6=\eps{width=5mm}{6wheel}$) and where $\exp_\udot$ means `exponential in the disjoint union sense'. \end{theorem}
Closed form formulas have also been given for the Kontsevich integral of framed unknots, the Hopf link and Hopf chains~\Cite{Bar-Natan-Lawrence~04}{Bar-NatanLawrence:RationalSurgery} and for torus knots~\Cite{Marche~04}{Marche:Computation}.
Theorem~\ref{thm:Wheels} has a companion that utilizes the same element $\Omega$, the ``wheeling theorem~\Cite{Bar-Natan-Garoufalidis-Rozansky-Thurston~00, Bar-Natan-Le-Thurston~03}{Bar-NatanGaroufalidisRozanskyThurston:WheelsWheeling, Bar-NatanLeThurston:TwoApplications}. The wheeling theorem ``upgrades the vector space isomorphism $\chi:\calB\to\calA$ to an algebra isomorphism and is related to the Duflo isomorphism of the theory of Lie algebras. It is amusing to note that the wheeling theorem (and hence Duflo's theorem in the metrized case) follows using finite type techniques from the ``$1+1=2$ on an abacus identity \[ \eps{width=2.6in}{Abacus}. \]
Taming the Kontsevich Integral
While explicit calculations are rare, there is a nice structure theorem for the values of the Kontsevich integral, saying that for a knot $K$ and up to any fixed number of loops in the Jacobi diagrams, $\chi^{-1}Z_1(K)$ can be described by finitely many rational functions (with denominators powers of the Alexander polynomial) which dictate the placement of the legs. This structure theorem was conjectured in~\Cite{Rozansky~03}{Rozansky:RationalityConjecture}, proven in~\Cite{Kricker~00}{Kricker:RationalityConjecture} and partially generalized to links in~\Cite{Garoufalidis-Kricker~04}{GaroufalidisKricker:NonCommutativeInvariant}.
The Rozansky-Witten theory
One way to construct linear functionals on $\calA$ (and hence finite type invariants) is using Lie algebras and representations as in Section~\ref{subsec:Jacobi}; much of our insight about $\calA$ comes this way. But there is another construction for such functionals (and hence invariants), due to Rozansky and Witten~\Cite{Rozansky-Witten~97}{RozanskyWitten:HyperKahler}, using contractions of curvature tensors on hyper-K\"ahler manifolds. Very little is known about the Rozansky-Witten approach; in particular, it is not known if it is stronger or weaker than the Lie algebraic approach. For an application of the Rozansky-Witten theory back to hyper-K\"ahler geometry check~\cite{HitchinSawon:HyperKahler} and for a unification of the Rozansky-Witten approach with the Lie algebraic approach (albeit at a categorical level) check~\Cite{Roberts-Willeton (in preparation)}{RobertsWillerton:InPreparation}.
The Melvin-Morton conjecture and the volume conjecture
The Melvin-Morton conjecture (stated~\Cite{Melvin-Morton~95}{MelvinMorton:Coloured}, proven~\Cite{Bar-Natan-Garoufalidis~96}{Bar-NatanGaroufalidis:MMR}) says that the Alexander polynomial can be read off certain coefficients of the coloured Jones polynomial. The Kashaev-Murakami-Murakami volume conjecture (stated~\cite{Kashaev:HyperbolicVolume, MurakamiMurakami:SimplicialVolume}, unproven) says that a certain asymptotic growth rate of the coloured Jones polynomial is the hyperbolic volume of the knot complement.
Both conjectures are not directly about finite type invariants but both have ramifications to the theory of finite type invariants. The Melvin-Morton conjecture was first proven using finite type invariants and several later proofs and generalizations (see~\cite{Bar-Natan:VasBib}) also involve finite type invariants. The volume conjecture would imply, in particular, that the hyperbolic volume of a knot complement can be read from that knot's finite type invariants, and hence finite type invariants would be at least as strong as the volume invariant.
A particularly noteworthy result and direction for further research is Gukov's~\cite{Gukov:APolynomial} recent unification of these two conjectures under the Chern-Simons umbrella (along with some relations to three dimensional quantum gravity).
Beyond knots
\label{sec:BeyondKnots} For the lack of space we have restricted ourselves here to a discussion of finite type invariants of knots. But the basic ``differentiation idea of Section~\ref{sec:intro} calls for generalization, and indeed it has been generalized extensively. We will only make a few quick comments.
Finite type invariants of homotopy links (links where each component is allowed to move across itself freely) and of braids are extremely well behaved. They separate, they all come from Lie algebraic constructions~\Cite{Bar-Natan~95,~96, Lin~97}{Bar-Natan:Homotopy, Lin:Expansions, Bar-Natan:Braids} and in the case of braids, step by step integration as in Section~\ref{subsec:StepByStep} works~\Cite{Hutchings~98}{Hutchings:SingularBraids} (for homotopy links the issue was not studied). Finite type invariants of 3-manifolds and especially of integral and rational homology spheres have been studied extensively and the picture is nearly a complete parallel of the picture for knots. There are several competing definitions of finite type invariants (due to \Cite{Ohtsuki~96}{Ohtsuki:IntegralHomology} and then \Cite{Goussarov~99, Garoufalidis~96, Garoufalidis-Goussarov-Polyak~01}{Goussarov:3Manifolds, Garoufalidis:3ManifoldsI, GaroufalidisGoussarovPolyak:Clovers} and more), and they all agree up to regrading. There are weight systems and they are linear functionals on a space $\calA(\emptyset)$ which is a close cousin of $\calA$ and $\calB$ and is related to Lie algebras and hyper-K\"ahler manifolds in a similar way. There is a notion of a ``universal invariant, and there are several constructions (due to \Cite{Le-Murakami-Ohtsuki~98, Le~96}{LeMurakamiOhtsuki:Universal, Le:UniversalIHS} and then \Cite{Bar-Natan-Garoufalidis-Rozansky-Thurston~02, 02, 04, Kuperberg-Thurston~99}{Bar-NatanGaroufalidisRozanskyThurston:Aarhus, KuperbergThurston:CutAndPaste}), they all agree or are conjectured to agree, and they are related to the Chern-Simons-Witten theory.
Finite type invariants were studied for several other types of topological objects, including knots within other manifolds, higher dimensional knots, virtual knots, plane curves and doodles and more. See~\cite{Bar-Natan:VasBib}.
References
\item[] The reference~\cite{Bar-Natan:VasBib} is an extensive bibliography of finite type invariants, listing more than \ifemp{550}{500 further} references. \ifemp{To save space, references for this article that appear in~\cite{Bar-Natan:VasBib} are only cited above stating the authors' full last name(s) and approximate year of publication.}{}
\ifemp{}{% 1997 \bibitem[AF]{AltschulerFreidel:AllOrders} D.~Altschuler and L.~Freidel,
{\em Vassiliev knot invariants and Chern-Simons perturbation theory
to all orders,}
Comm.{} Math.{} Phys.{} {\bf 187} (1997) 261--287, \arXiv{q-alg/9603010}.
}
\ifemp{}{% 1991 \bibitem[BN1]{Bar-Natan:Thesis} D.~Bar-Natan,
{\em Perturbative aspects of the Chern-Simons topological quantum
field theory},
Ph.D.{} thesis, Princeton Univ., June 1991.
}
[Bar-Natan_95] ^ D. Bar-Natan, On the Vassiliev knot invariants, Topology 34 (1995) 423-472.
\ifemp{}{% 1995 \bibitem[BN3]{Bar-Natan:Homotopy} D.~Bar-Natan,
{\em Vassiliev homotopy string link invariants,}
Jour.{} of Knot Theory and its Ramifications {\bf 4} (1995) 13--32.
}
[Bar-Natan_96] ^ D. Bar-Natan, Some computations related to Vassiliev invariants, electronic publication, http://www.math.toronto.edu/~drorbn/LOP.html#Computations.
[Bar-Natan_97] ^ D. Bar-Natan, Non-associative tangles, in Geometric topology (proceedings of the Georgia international topology conference), (W. H. Kazez, ed.), 139-183, Amer. Math. Soc. and International Press, Providence, 1997.
\ifemp{\bibitem[BN1]{Bar-Natan:VasBib}}{\bibitem[BN6]{Bar-Natan:VasBib}}
D.~Bar-Natan, {\em Bibliography of Vassiliev invariants,}
{\tt http://\linebreak[0]www.math.toronto.edu/\linebreak[0]$\sim$drorbn/\lineb
reak[0]VasBib}.
\ifemp{}{% 1996
\bibitem[BN7]{Bar-Natan:Braids} D.~Bar-Natan,
{\em Vassiliev and quantum invariants of braids,}
in Proc.{} of Symp.{} in Appl.{} Math.{} {\bf 51} (1996) 129--144,
{\em The interface of knots and physics,} (L.~H.~Kauffman, ed.),
Amer.{} Math.{} Soc., Providence.
}
\ifemp
{\bibitem[BN2]{Bar-Natan:Associators}}
{\bibitem[BN8]{Bar-Natan:Associators}}
D.~Bar-Natan, {\em On Associators and the Grothendieck-Teichmuller Group I,}
Selecta Mathematica, New Series {\bf 4} (1998) 183--212.
\ifemp{}{% 2000 \bibitem[BN9]{Bar-Natan:AstrologyToTopology} D.~Bar-Natan,
{\em From astrology to topology via Feynman diagrams and Lie algebras,}
Rendiconti Del Circolo Matematico Di Palermo Serie II {\bf 63} (2000)
11--16, {\tt
http:\linebreak[0]//\linebreak[0]www.math.toronto.edu/\linebreak[0]$\sim$drorb
n/\linebreak[0]Talks/\linebreak[0]Srni-9901}. }
\ifemp{}{% 2001 \bibitem[BN10]{Bar-Natan:Bracelets} D.~Bar-Natan,
{\em Bracelets and the Goussarov filtration of the space of knots,}
{\em Invariants of knots and 3-manifolds (Kyoto 2001),} Geometry and
Topology Monographs {\bf 4} 1--12, \arXiv{math.GT/0111267}.
}
\ifemp{}{% 1996 \bibitem[BNG]{Bar-NatanGaroufalidis:MMR} D.~Bar-Natan and S.~Garoufalidis,
{\em On the Melvin-Morton-Rozansky conjecture,}
Invent.{} Math.{} {\bf 125} (1996) 103--133.
}
\ifemp{}{% 2000 \bibitem[BGRT1]{Bar-NatanGaroufalidisRozanskyThurston:WheelsWheeling}
D.~Bar-Natan, S.~Garoufalidis, L.~Rozansky and D.~P.~Thurston,
{\em Wheels, wheeling, and the Kontsevich integral of the unknot,}
Israel Journal of Mathematics {\bf 119} (2000) 217--237,
\arXiv{q-alg/9703025}.
}
\ifemp{}{% 2002, 2002, 2004 \bibitem[BGRT2]{Bar-NatanGaroufalidisRozanskyThurston:Aarhus}
D.~Bar-Natan, S.~Garoufalidis, L.~Rozansky and D.~P.~Thurston,
{\em The \AA{}rhus integral of rational homology 3-spheres I--III,}
Selecta Mathematica, New Series {\bf 8} (2002) 315--339,
\arXiv{q-alg/9706004}, {\bf 8} (2002) 341--371,
\arXiv{math.QA/9801049}, to appear, \arXiv{math.QA/9808013}.
}
\ifemp{}{% 2004 \bibitem[BNL]{Bar-NatanLawrence:RationalSurgery} D.~Bar-Natan and
R.~Lawrence,
{\em A Rational Surgery Formula for the LMO Invariant,}
Israel Journal of Mathematics {\bf 140} (2004) 29--60,
\arXiv{math.GT/0007045}.
}
[Bar-Natan_Le_Thurston_03] ^ D. Bar-Natan, T. Q. T. Le and D. P. Thurston, Two applications of elementary knot theory to Lie algebras and Vassiliev invariants, Geometry and Topology 7-1 (2003) 1-31, arXiv:math.QA/0204311.
\bibitem[BNT]{Bar-NatanThurston:AlgebraicStructures} D.~Bar-Natan and
D.~Thurston,
{\em Algebraic Structures on Knotted Objects and Universal Finite Type
Invariants,}
in prepartion, {\tt
http:\linebreak[0]//\linebreak[0]www.math.toronto.edu/\linebreak[0]$\sim$drorb
n/\linebreak[0]papers/\linebreak[0]AlgebraicStructures}.
[Birman_Lin_93] ^ J. S. Birman and X.-S. Lin, Knot polynomials and Vassiliev's invariants, Invent. Math. 111 (1993) 225-270.
\ifemp{}{% 1994 \bibitem[BoTa]{BottTaubes:SelfLinking} R.~Bott and C.~Taubes,
{\em On the self-linking of knots},
Jour.{} Math.{} Phys.{} {\bf 35} (1994).
}
[Broadhurst_97] ^ D. J. Broadhurst, Conjectured enumeration of Vassiliev invariants, preprint, September 1997, arXiv:q-alg/9709031.
\ifemp{}{% 2001 \bibitem[CD]{ChmutovDuzhin:KontsevichIntegral} S.~V.~Chmutov and
S.~V.~Duzhin,
{\em The Kontsevich integral,}
Acta Applicandae Mathematicae {\bf 66} (2001) 155--190.
}
[Chmutov_Duzhin_Lando_94] ^ S. V. Chmutov, S. V. Duzhin and S. K. Lando, Vassiliev knot invariants I. Introduction, in Adv. in Soviet Math., 21 (1994) Singularities and curves, (V. I. Arnold, ed.), 117-126.
\ifemp{}{% 2003 \bibitem[Co]{Conant:OnGoussarov} J.~Conant,
{\em On a theorem of Goussarov,}
Jour.{} of Knot Theory and its Ramifications {\bf 12-1} (2003) 47--52,
\arXiv{math.GT/0110057}.
}
[Dasbach_00] ^ O. T. Dasbach, On the combinatorial structure of primitive Vassiliev invariants III - a lower bound, Comm. in Cont. Math. 2-4 (2000) 579-590, arXiv:math.GT/9806086.
[Drinfeld_90] ^ V. G. Drinfel'd, Quasi-Hopf algebras, Leningrad Math. J. 1 (1990) 1419-1457.
[Drinfeld_91] ^ V. G. Drinfel'd, On quasitriangular Quasi-Hopf algebras and a group closely connected with , Leningrad Math. J. 2 (1991) 829-860.
\ifemp{}{% 1996 \bibitem[Ga]{Garoufalidis:3ManifoldsI} S.~Garoufalidis,
{\em On finite type 3-manifold invariants I,}
Jour.{} of Knot Theory and its Ramifications {\bf 5} (1996) 441--462.
}
\ifemp{}{% 2001 \bibitem[GGP]{GaroufalidisGoussarovPolyak:Clovers} S.~Garoufalidis,
M.~Goussarov and M.~Polyak,
{\em Calculus of clovers and finite type invariants of 3-manifolds,}
Geometry and Topology {\bf 5-3} (2001) 75--108, \arXiv{math.GT/0005192}.
}
\ifemp{}{% 2004 \bibitem[GK]{GaroufalidisKricker:NonCommutativeInvariant} S.~Garoufalidis
and A.~Kricker,
{\em A rational noncommutative invariant of boundary links,}
Geometry and Topology {\bf 8-4} (2004) 115--204, \arXiv{math.GT/0105028}.
}
[Goussarov_91] ^ M. Goussarov, A new form of the Conway-Jones polynomial of oriented links, Zapiski nauch. sem. POMI 193 (1991) 4-9 (English translation in Topology of manifolds and varieties (O.~Viro, editor), Amer. Math. Soc., Providence 1994, 167-172).
[Goussarov_93] ^ M. Goussarov, On -equivalence of knots and invariants of finite degree, Zapiski nauch. sem. POMI 208 (1993) 152-173 (English translation in Topology of manifolds and varieties (O. Viro, editor), Amer. Math. Soc., Providence 1994, 173-192).
\ifemp{}{% 1998 \bibitem[Go3]{Goussarov:Modifications} M.~Goussarov,
{\em Interdependent modifications of links and invariants of finite
degree,}
Topology {\bf 37-3} (1998) 595--602.
}
\ifemp{}{% 1998 \bibitem[Go4]{Goussarov:PresentedByGauss} M.~Goussarov,
{\em Finite type invariants are presented by Gauss diagram formulas,}
preprint (translated from Russian by O.~Viro), December 1998, {\tt
http:\linebreak[0]//\linebreak[0]www.math.toronto.edu/\linebreak[0]$\sim$drorb
n/\linebreak[0]Goussarov/}. }
\ifemp{}{% 1999 \bibitem[Go5]{Goussarov:3Manifolds} M.~Goussarov,
{\em Finite type invariants and $n$-equivalence of 3-manifolds,}
C.{} R.{} Acad.{} Sci.{} Paris S\'er.{} I Math.{} {\bf 329(6)} (1999)
517--522.
}
\ifemp{}{% 2000 \bibitem[GPV]{GoussarovPolyakViro:VirtualKnots} M.~Goussarov, M.~Polyak and
O.~Viro,
{\em Finite type invariants of classical and virtual knots,}
Topology {\bf 39} (2000) 1045--1068, \arXiv{math.GT/9810073}.
}
\bibitem[Gu]{Gukov:APolynomial} S.~Gukov,
{\em Three-dimensional quantum gravity, Chern-Simons theory, and the
A-polynomial,}
preprint, \arXiv{hep-th/0306165}.
\ifemp{}{% 2000 \bibitem[Ha]{Habiro:Claspers} K.~Habiro,
{\em Claspers and finite type invariants of links,}
Geometry and Topology {\bf 4} (2000) 1--83.
}
\bibitem[HS]{HitchinSawon:HyperKahler} N.~Hitchin and J.~Sawon,
{\em Curvature and characteristic numbers of hyperkähler manifolds,}
Duke Math.{} Jour.{} {\bf 106-3} (2001) 599--615,
\arXiv{math.DG/9908114}.
\ifemp{}{% 1998 \bibitem[Hu]{Hutchings:SingularBraids} M.~Hutchings,
{\em Integration of singular braid invariants and graph cohomology,}
Transactions of the AMS {\bf 350} (1998) 1791--1809.
}
\bibitem[Ka]{Kashaev:HyperbolicVolume} R.~M.~Kashaev,
{\em The hyperbolic volume of knots from quantum dilogarithm,}
Lett.{} Math.{} Phys.{} {\bf 39} (1997) 269--275, \arXiv{q-alg/9601025}.
[Kneissler_97] ^ J. A. Kneissler, The number of primitive Vassiliev invariants up to degree twelve, preprint, June 1997, arXiv:q-alg/9706022.
\bibitem[KZ]{KnizhnikZamolodchikov:CurrentAlgebra} V.~G. Knizhnik and
A.~B. Zamolodchikov,
{\em Current algebra and Wess-Zumino model in two dimensions,}
Nucl.{} Phys.{} {\bf B247} (1984) 83--103.
[Kontsevich_93] ^ M. Kontsevich, Vassiliev's knot invariants, Adv. in Sov. Math., 16(2) (1993) 137-150.
\ifemp{}{% 1994 \bibitem[Ko2]{Kontsevich:FeynmanDiagrams} M.~Kontsevich,
{\em Feynman diagrams and low-dimensional topology,}
First European Congress of Mathematics {\bf II} 97--121, Birkh\"auser
Basel 1994.
}
[Kontsevich] ^ M. Kontsevich, unpublished.
\ifemp{}{% 2000 \bibitem[Kr]{Kricker:RationalityConjecture} A.~Kricker,
{\em The lines of the Kontsevich integral and Rozansky's rationality
conjecture,}
preprint, May 2000, \arXiv{math.GT/0005284}.
}
\ifemp{}{% 1999 \bibitem[KT]{KuperbergThurston:CutAndPaste} G.~Kuperberg and
D.~P.~Thurston,
{\em Perturbative 3-manifold invariants by cut-and-paste topology,}
preprint, December 1999, \arXiv{math.GT/9912167}.
}
\ifemp{}{% 1996 \bibitem[Le]{Le:UniversalIHS} T.~Q.~T.~Le,
{\em An invariant of integral homology 3-spheres which is universal
for all finite type invariants,}
in {\em Solitons, geometry and topology: on the crossroad},
(V.~Buchstaber and S.~Novikov, eds.) AMS Translations Series 2,
Providence, \arXiv{q-alg/9601002}.
}
\ifemp{}{% 1995 \bibitem[LM1]{LeMurakami:HOMFLY} T.~Q.~T.~Le and J.~Murakami,
{\em On Kontsevich's integral for the HOMFLY polynomial and
relations of multiple $\zeta$-numbers,}
Topology and its Applications {\bf 62} (1995) 193--206.
}
[Le_Murakami_96] ^ T. Q. T. Le and J. Murakami, The universal Vassiliev-Kontsevich invariant for framed oriented links, Compositio Math. 102 (1996), 41-64, arXiv:hep-th/9401016.
\ifemp{}{% 1998 \bibitem[LMO]{LeMurakamiOhtsuki:Universal} T.~Q.~T.~Le, J.~Murakami and
T.~Ohtsuki,
{\em On a universal quantum invariant of 3-manifolds,}
Topology {\bf 37-3} (1998) 539--574, \arXiv{q-alg/9512002}.
}
\ifemp{}{% 2001 \bibitem[Les]{Lescop:ForLinks} C.~Lescop,
{\em On configuration space integrals for links,}
{\em Invariants of knots and 3-manifolds (Kyoto 2001),} Geometry and
Topology Monographs {\bf 4} 183-199, \arXiv{math.GT/0211062}.
}
[Lieberum_99] ^ J. Lieberum, On Vassiliev invariants not coming from semisimple Lie algebras, Journal of Knot Theory and its Ramifications 8-5 (1999) 659-666, arXiv:q-alg/9706005.
\ifemp{}{% 2002 \bibitem[Lie2]{Lieberum:gl11} J.~Lieberum,
{\em The Drinfeld associator of $gl(1|1)$,}
preprint, April 2002, \arXiv{math.QA/0204346}.
}
[Lin_91] ^ X-S. Lin, Vertex models, quantum groups and Vassiliev's knot invariants, preprint, 1991, [1].
\ifemp{}{% 1997 \bibitem[Lin2]{Lin:Expansions} X-S. Lin,
{\em Power series expansions and invariants of links,}
in {\em Geometric topology} (proceedings of the Georgia international
topology conference), (W.~H.~Kazez, ed.), 184--202, Amer.{} Math.{}
Soc.{} and International Press, Providence, 1997.
}
\ifemp{}{% 2004 \bibitem[Ma]{Marche:Computation} J.~Marche,
{\em A computation of Kontsevich integral of torus knots,}
preprint, April 2004, \arXiv{math.GT/0404264}.
}
\ifemp{}{% 1995 \bibitem[MeMo]{MelvinMorton:Coloured} P.~M.~Melvin and H.~R.~Morton,
{\em The coloured Jones function,}
Comm.{} Math.{} Phys.{} {\bf 169} (1995) 501--520.
}
\ifemp
{\bibitem[MM]{MurakamiMurakami:SimplicialVolume}}
{\bibitem[MuMu]{MurakamiMurakami:SimplicialVolume}}
J.~Murakami and H.~Murakami,
{\em The colored Jones polynomials and the simplicial volume of a knot,}
Acta Math.{} {\bf 186-1} (2001) 85--104, \arXiv{math.GT/9905075}.
\ifemp{}{% 1998 \bibitem[Ng]{Ng:Ribbon} K.~Y.~Ng,
{\em Groups of ribbon knots,}
Topology {\bf 37} (1998) 441--458, \arXiv{q-alg/9502017} (with an
addendum at \arXiv{math.GT/0310074}).
}
\ifemp{}{% 1999 \bibitem[NS]{NgStanford:GusarovGroup} K.~Y.~Ng and T.~Stanford,
{\em On Gusarov's groups of knots,}
Proc.{} Camb.{} Phil.{} Soc.{} {\bf 126-1} (1999) 63--76.
}
\ifemp{}{% 1996 \bibitem[Oh]{Ohtsuki:IntegralHomology} T.~Ohtsuki,
{\em Finite type invariants of integral homology 3-spheres,}
Jour.{} of Knot Theory and its Ramifications {\bf 5(1)} (1996) 101--115.
}
\ifemp{}{% 1999 \bibitem[Po]{Poirier:LimitConfigurationSpace} S.~Poirier,
{\em The limit configuration space integral for tangles and the
Kontsevich integral,}
preprint, February 1999, \arXiv{math.GT/9902058}.
}
[Reshetikhin_Turaev_90] ^ N. Yu. Reshetikhin and V. G. Turaev, Ribbon graphs and their invariants derived from quantum groups, Commun. Math. Phys. 127 (1990) 1-26.
\ifemp{}{% in preparation \bibitem[RobWil]{RobertsWillerton:InPreparation} J.~Roberts and
S.~Willeton, in preparation.
}
\ifemp{}{% 2003 \bibitem[Ro]{Rozansky:RationalityConjecture} L.~Rozansky,
{\em A rationality conjecture about Kontsevich integral of knots and
its implications to the structure of the colored Jones polynomial,}
Proccedings of the Pacific Institute for the Mathematical Sciences
Workshop (Calgary 1999), Topology and its Applications {\bf 127} (2003)
47--76, \arXiv{math.GT/0106097}.
}
\ifemp{}{% 1997 \bibitem[RozWit]{RozanskyWitten:HyperKahler} L.~Rozansky and E.~Witten,
{\em Hyper-K\"ahler geometry and invariants of three-manifolds,}
Selecta Mathematica, New Series, {\bf 3} (1997) 401--458,
\arXiv{hep-th/9612216}.
}
\ifemp{}{% 1998 \bibitem[Sta]{Stanford:ModuloPureBraids} T.~Stanford,
{\em Vassiliev invariants and knots modulo pure braid subgroups,}
preprint, May 1998, \arXiv{math.GT/9805092}.
}
[Stoimenow_98] ^ A. Stoimenow, Enumeration of chord diagrams and an upper bound for Vassiliev invariants, Jour. of Knot Theory and its Ramifications 7(1) (1998) 94-114.
\ifemp{}{% 1995 \bibitem[Th1]{Thurston:IntegralExpressions} D.~Thurston,
{\em Integral expressions for the Vassiliev knot invariants,}
Harvard University senior thesis, April 1995, \arXiv{math.QA/9901110}.
}
\ifemp{}{% 2001 \bibitem[Th2]{Thurston:Shadow} D.~Thurston,
{\em The algebra of knotted trivalent graphs and Turaev's shadow world,}
{\em Invariants of knots and 3-manifolds (Kyoto 2001),} Geometry and
Topology Monographs {\bf 4} 337--362, \arXiv{math.GT/0311458}.
}
[Vassiliev_90] ^ V. A. Vassiliev, Cohomology of knot spaces, in Theory of Singularities and its Applications (Providence) (V. I. Arnold, ed.), Amer. Math. Soc., Providence, 1990.
[Vassiliev_92] ^ V. A. Vassiliev, Complements of discriminants of smooth maps: topology and applications, Trans. of Math. Mono. 98, Amer. Math. Soc., Providence, 1992.
[Vogel_97] ^ P. Vogel, Algebraic structures on modules of diagrams, preprint, July 1995 (revised 1997), http://www.math.jussieu.fr/~vogel/.
[Vogel_99] ^ P. Vogel, The universal Lie algebra, preprint, June 1999, http://www.math.jussieu.fr/~vogel/.
\ifemp{}{% 2004 \bibitem[Vol]{Volic:TaylorTowers} I.~Volic,
{\em Configuration space integrals and Taylor towers for spaces of knots,}
preprint, January 2004, \arXiv{math.GT/0401282}.
}
[Willerton_96] ^ S. Willerton, Vassiliev invariants and the Hopf algebra of chord diagrams, Math. Proc. Camb. Phil. Soc. 119 (1996) 55-65.
\ifemp{\bibitem[Wi]{Witten:Jones}}{\bibitem[Wit]{Witten:Jones}}
E. Witten, {\em Quantum field theory and the Jones polynomial,}
Commun.{} Math.{} Phys.{} {\bf 121} (1989) 351--399.
\ifemp{}{% 1997 \bibitem[Ya]{Yang:DegreeTheory} S.-W.~Yang,
{\em Feynman integral, knot invariant and degree theory of maps,}
preprint, September 1997, \arXiv{q-alg/9709029}.
}
[Zagier_01] ^ D. Zagier, Vassiliev invariants and a strange identity related to the Dedekind eta-function, Topology 40(5) (2001) 945-960.



















































![{\displaystyle [x,y]=xy-yx}](https://wikimedia.org/api/rest_v1/media/math/render/svg/42b4220c8122ebd2a21c517ca80639581679cfa6)







