10-1100/Assignment 1 Part 1 by Charles

Pyraminx by Charles Tsang

In this article, we will analyze Pyraminx, a variant of the Rubik's cube. We will restrict our attention to those permutations which can only be generated by turning the sides of the puzzle (not by “cheating” and reassembling the puzzle).

As an introduction, we shall describe the shape of the puzzle. It is shaped as a tetrahedron. i.e. It has 4 faces at which each face is a equilateral triangle with a different solid colour. And on each face, it is composed of 9 smaller equilateral triangles. The following are pictures of the puzzle and its decomposition into a net.

The faces are coloured green, blue, orange and yellow, and each smaller equilateral triangle is labelled with numbers.

Now we are ready to play!

To understand the puzzle, we need to observe what happens to the numbers when we turn each face.

When we turn the green face [“clockwise” with respect to the net], the number 1 is now in place of 5, and 5 goes to 25 etc... (At first this seems easy but because this is a tetrahedron, it is actually more complicated than it seems. So to aid this process, I actually created several nets on different sheets of papers and created a tetrahedron to keep track of the permutations.) We write this as a permutaiton : [25,14,13,2,1,11,12,23,24,35,36,26,15,4,3,9,10,18,19,20,21,22,27,16,5,7,8,28,29,30,31,32,33,34,17,6 ] In this notation, the i'th term in the list correspond to the iverse image of number i under turning the green face.

Repeat the same procedure for blue, orange and yellow, we can see that they represent the permutations [1,2,3,35,36,26,25,14,9,10,11,12,13,33,34,28,27,16,15,4,21,22,23,24,32,30,29,18,17,6,5,7,8,19,20,31] [6,17,18,29,30,32,31,20,19,8,7,5,13,14,15,16,33,22,21,10,9,3,4,24,25,26,27,28,23,12,11,1,2,34,35,36] and [31,20,3,4,5,6,7,8,9,29,30,32,21,10,15,16,17,18,19,27,28,34,33,22,11,1,2,13,14,25,26,36,35,24,23,12] respectively.

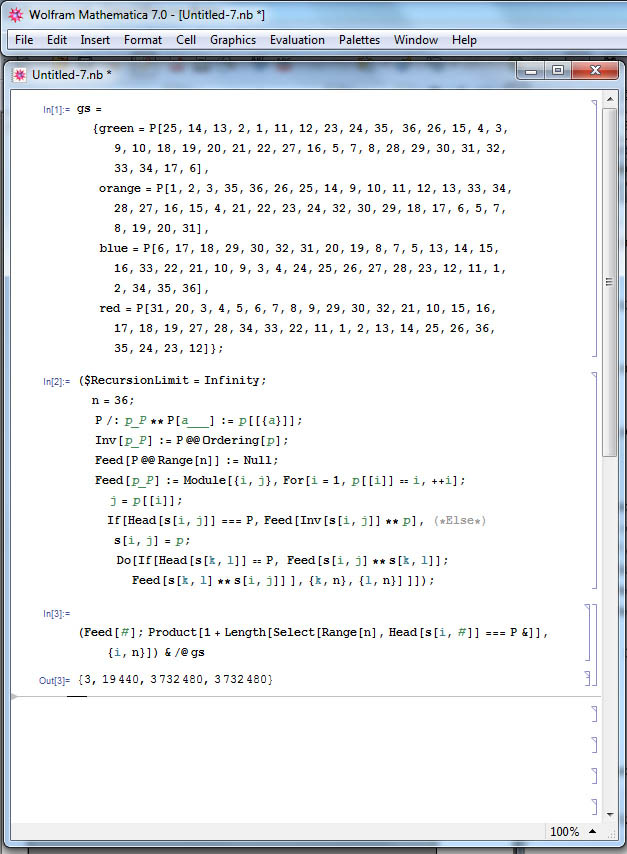
Then after running the Schreier–Sims algorithm in Mathematica, we have found that there are 3,732,480 different configurations by turning each face of the puzzle. More specifically, if we restrict ourselves into only turning one side in the beginning, we get 3 different configurations, and if we restrict ourselves into turn two sides, we get 19440 configurations, which we can readily see from the output.

Here is the input/output log for those who are interested:

I hope everyone has enjoyed it as much as I did analyzing it!