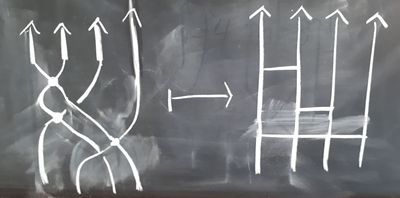Notes for AKT-140127/0:47:34

This note closely follows the introductory parts of "Vassiliev and Quantum Invariants of Braids" by Dror Bar-Natan (1996).

The notion of finite type invariant can be extended to different knot-like objects (braids, tangles, links, etc.). While it is an open question whether finite type invariants separate knots, it is known that finite type invariants separate braids. In this note, we describe the process of getting a chord diagram from an m-singular braid, as well as describing the framework in which one would perform a similar analysis to the one done in lecture on braids.

Given a braid $B$ with n strands and m double points, the chord diagram $D_B$ is given as illustrated below (with $n$ = 4 and $m$ = 3).

It is clear how to do this for all $n$, $m$. The space of $m$-chord pure braid diagrams then forms a space $\mathcal{D}^{pb}_m$, and just as in the case of knots, given a type $m$ invariant $V$ of braids with $n$ strands with values in an abelian group $A$, there is a map $W_V: \mathcal{D}^{pb}_m \rightarrow A$ defined by $W_V(D) = V(B)$, where $D_B = D$. Then define $\mathcal{D}^{pb}$ as the completed direct sum of all $\mathcal{D}^{pb}_m$, and define $\mathcal{A}^{pb}$ as $\mathcal{D}^{pb}/\mathcal{I}$, where $\mathcal{I}$ is an ideal generated by relations among braid chord diagrams analogous to the FI and 4T relations of the familiar knot chord diagrams. If one continues with this analysis, one can find that finite type invariants in fact do separate braids. For a proof of this fact and much more detail regarding the above, see https://www.math.toronto.edu/drorbn/papers/glN/glN.pdf.