Mutation Invariance of Khovanov Homology

The purpose of this note is to sketch my "almost proof" of mutation invariance for Khovanov homology and to discuss "re-imbedding invariance" for Khovanov homology.

History And Summary

I have presented an almost-proof of invariance of Khovanov homology under knot mutation in a conference in Snowbird, Utah in June 2005 (see the handouts from that talk here). At the time it was clear to me that the very end of the proof is a bit fishy, and an example by Jake Rasmussen made it look even fishier.

Yet the proof seemed to have all the right ingredients in it (for example, it was restricted to the case of knots; indeed, mutation invariance of Khovanov homology for links is known to fail). So I was quite sure the missing bit will be completed quickly. A short time later I (thought I) was able to complete the proof, and for a few months I believed my proof was right, though I did not write it up so I was never confident.

Then in October 2005 I explained my proof over the phone to Stephan Wehrli in Zurich, and in December 2005 he contacted me again with a gap in the proof. I still don't know how to resolve the difficulty and I am no longer convinced that Khovanov homology is invariant under knot mutation.

Yet not all is lost:

• The proof remains "almost true" and still seems to have (at least most of) the right ingredients. Thus somebody may well be able to complete it one day.

• The parts of the proof that still hold suggest ways to narrow down the search for counterexamples for mutation invariance. Thus with the proper software there is some real hope that a counterexample will be found.

• In an effort to save the proof I realized that mutation invariance is implied by a much broader and more conceptual suggested property of Khovanov homology, the property of "re-imbedding invariance". The difficulty in proving re-imbedding invariance is the same as the difficulty in proving mutation invariance, but the benefit, if proven, seems greater. I hope people will put some effort into understanding re-imbedding invariance.

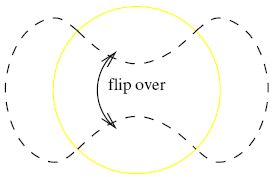
What's Mutation?

A mutation is the process of marking a circle on a knot or a link diagram which intersects it at precisely four points, and flipping its inside (and not its outside!) around a horizontal axis as illustrated on the right. (Other types of mutation are topologically equivalent to this one). Mutation does not change the overall connectivity of the knot/link in question. Thus a knot stays a knot and a link stays a link.

It is well known that the Jones polynomial (as well as the Alexander, HOMFLYPT, and coloured Jones polynomials) is invariant under knot mutation. There are easy examples to show that Khovanov homology is not invariant under link mutation, but it is still unknown whether or not Khovanov homology is invariant under knot mutation.