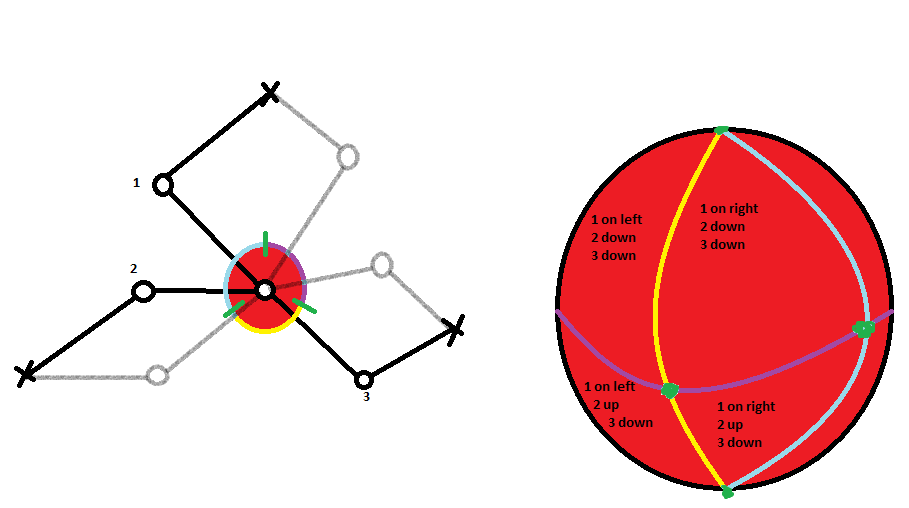
10-327/Solution to configuration of a 3 legged spider
From Drorbn
Jump to navigationJump to search
It's a sphere. Divide the sphere into 8 section, and have the middle joint denote where on each section a configuration relates to. Then label each section by how the joints are bent (up or down, left or right). If the middle joint is at the boundary of where it can move then one of the joints must be straight (both up and down) and can move from one section to another by small permutations. Hopefully this makes sense. I believe you can also prove it by looking at the "level sets" of the configuration, by fixing one joint and looking at the "sub"-configuration space. (Like how the sphere was done in class) -John
Well done! Now what about the 4-legged spider? Drorbn 22:09, 24 November 2010 (EST)