User:Zsuzsi/HW4

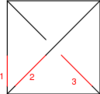
The Generators

Our generators are $T$, $R$, $\Phi$ and $B^{\pm }$:

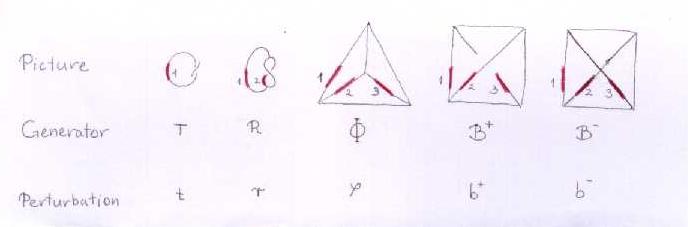
Picture
Generator	$T$	$R$	$\Phi$	$B^{+}$	$B^{-}$
Perturbation	$t$	$r$	$\varphi$	$b^{+}$	$b^{-}$

A low-tech completed version of this chart:

The Relations

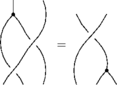
The Reidemeister move R1

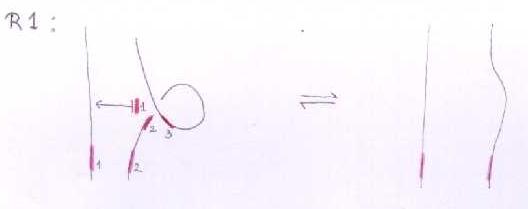
We cannot write this in the first notation, as the chords ending on both the second and third red line will end on the second pink line.

In the linearized functional notation, if I'm getting this right, it looks like this:

$\rho _{1}(x_{1},x_{2})=b^{-}(x_{1},x_{2},-x_{2})$

Where the negative sign is because the order of the chords is reversed as we slide them along the little loop.

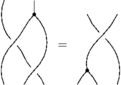
The Reidemeister move R2

With three sides of the shielding removed, the picture is:

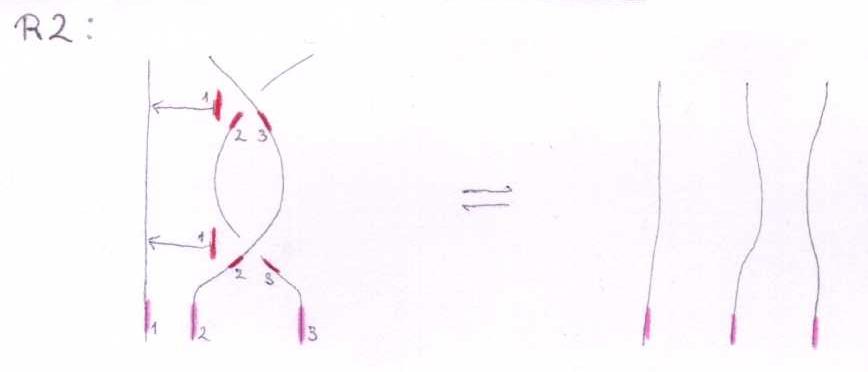
This means: $(123)^{\star }B^{+}(132)^{\star }B^{-}=1$

Linearized and in functional form:

$\rho _{2}(x_{1},x_{2},x_{3})=b^{+}(x_{1},x_{2},x_{3})+b^{-}(x_{1},x_{3},x_{2})$

((The right side won't contribute anything, right?))

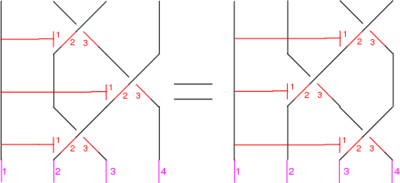
The Reidemeister Move R3

The picture (with three sides of the shielding removed) is

In formulas, this is

$(1230)^{\star }B^{+}(1213)^{\star }B^{+}(1023)^{\star }B^{+}=(1123)^{\star }B^{+}(1203)^{\star }B^{+}(1231)^{\star }B^{+}$.

Linearized and written in functional form, this becomes

$\rho _{3}(x_{1},x_{2},x_{3},x_{4})=$	$b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})$
	$-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).$

The Reidemeister Move R4, source:Andy

First version of R4:

In formulas, this is

$(1230)^{\star }B^{+}(1213)^{\star }B^{+}(1023)^{\star }\Phi =(1123)^{\star }\Phi (1233)^{\star }B^{+}$.

Linearized and written in functional form, this becomes

$\rho _{4a}(x_{1},x_{2},x_{3},x_{4})=b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+\phi (x_{1},x_{3},x_{4})-\phi (x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{3}+x_{4}).$

Second version:

In formulas, this is

$(1123)^{\star }B^{+}(1203)^{\star }B^{+}(1231)^{\star }\Phi =(1230)^{\star }\Phi (1223)^{\star }B^{+}$.

Linearized and written in functional form, this becomes

$\rho _{4b}(x_{1},x_{2},x_{3},x_{4})=b^{+}(x_{1}+x_{2},x_{3},x_{4})+b^{+}(x_{1},x_{2},x_{4})+\phi (x_{1}+x_{4},x_{2},x_{3})-\phi (x_{1},x_{2},x_{3})-b^{+}(x_{1},x_{2}+x_{3},x_{4}).$

The Syzygies

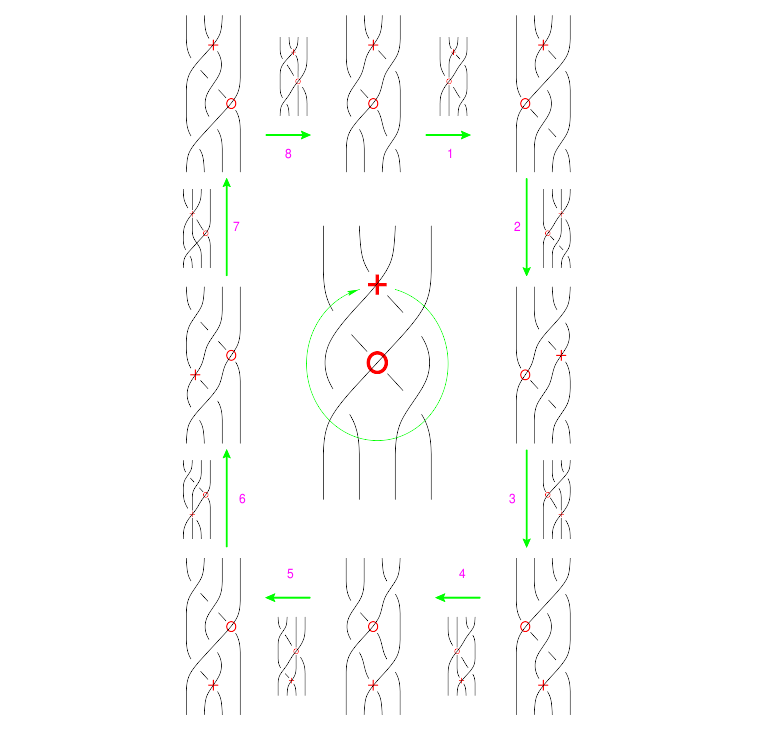
The "B around B" Syzygy

The picture, with all shielding removed, is

(Drawn with Inkscape) (note that lower quality pictures are also acceptable)

The functional form of this syzygy is

$BB(x_{1},x_{2},x_{3},x_{4},x_{5})=$	$\rho _{3}(x_{1},x_{2},x_{3},x_{5})+\rho _{3}(x_{1}+x_{5},x_{2},x_{3},x_{4})-\rho _{3}(x_{1}+x_{2},x_{3},x_{4},x_{5})$
	$-\rho _{3}(x_{1},x_{2},x_{4},x_{5})-\rho _{3}(x_{1}+x_{4},x_{2},x_{3},x_{5})-\rho _{3}(x_{1},x_{2},x_{3},x_{4})$
	$+\rho _{3}(x_{1},x_{3},x_{4},x_{5})+\rho _{3}(x_{1}+x_{3},x_{2},x_{4},x_{5}).$

A Mathematica Verification

The following simulated Mathematica session proves that for our single relation and single syzygy, $d^{2}=0$. Copy paste it into a live Mathematica session to see that it's right!

In[1]:=

d1 = { rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] }; d2 = { BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] };

In[3]:=	BAroundB[x1, x2, x3, x4, x5] /. d2
Out[3]=	- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] + rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4]

In[4]:=	BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
Out[4]=	0