06-1350/Syzygies in Asymptote in Brief

Installation

See 06-1350/Syzygies in Asymptote for more detailed information.

First install Asymptote. Once installed, download syzygy.asy.

Braids

import syzygy;  // Accesses the syzygy module.
Braid b;        // Start a new braid.
b.n=3;          // The braid has three strands.
                // The strands are numbered left to right starting at 0.
b.add(bp,0);    // Add a overcrossing component starting at strand 0,
                // the leftmost strand.
b.add(bm,1);    // Add an undercrossing starting at strand 1.
b.add(phi,0);   // Add a trivalent vertex that merges strands 0 and 1.
                // Strand 2 is now renumbered as strand 1.
b.draw();       // Draw the resulting braid.

Relations

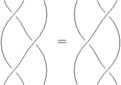
import syzygy;      // Access the syzygy module.
Braid l;            // Define the left hand side of the relation.
l.n=3;  l.add(bp,0);  l.add(bp,1);  l.add(bp,0);
Braid r;            // Define the right hand side of the relation.
r.n=3;  r.add(bp,1);  r.add(bp,0);  r.add(bp,1);

Relation r3;        // Define a relation.
r3.lsym="\rho_3";   // Give the relation a name for when it is written in functional form.
r3.codename="rho3"; // Give the relation a name to be used by Mathematica.
r3.lhs=l;  r3.rhs=r;
r3.draw();

r3.toFormula() produces the formula:

[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ }[/math]

r3.toLinear() produces the formula in linear form:

[math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3) }[/math]

and r3.toCode() produces a version usable in Mathematica:

rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4]
                            - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3]

Syzygies

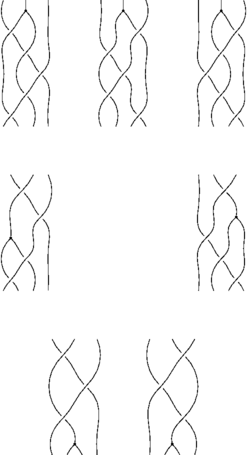
import syzygy;

// Phi around B
Braid initial;
initial.n=4;
initial.add(bp,2);
initial.add(bp,0);
initial.add(bp,1);
initial.add(bp,0);
initial.add(bp,2);
initial.add(phi,1);

Syzygy pb;
pb.lsym="\Phi B";
pb.codename="PhiAroundB";
pb.initial=initial;
pb.apply(r3,1,0);
pb.apply(r4a,3,1);
pb.swap(2,3);
pb.apply(r4b,0,1);
pb.apply(-r3,1,0);
pb.apply(-r4a,0,0);
pb.swap(2,3);
pb.apply(-r4b,3,0);
pb.apply(r3,1,1);

pb.draw();

Again, like relations, we can use pb.toLinear()

[math]\displaystyle{ \Phi B(x_1,x_2,x_3,x_4,x_5) = }[/math]	[math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_5) + \rho_{4a}(x_1+x_5,x_2,x_3,x_4) + \rho_{4b}(x_1+x_2,x_3,x_4,x_5) }[/math]
	[math]\displaystyle{ - \rho_3(x_1,x_2,x_3+x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4) }[/math]
	[math]\displaystyle{ - \rho_{4b}(x_1,x_3,x_4,x_5) + \rho_3(x_1+x_3,x_2,x_4,x_5). }[/math]

and pb.toCode()

PhiAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho4a[x1 + x5, x2, x3, x4]
 + rho4b[x1 + x2, x3, x4, x5] - rho3[x1, x2, x3 + x4, x5] - rho4a[x1, x2, x3, x4]
 - rho4b[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5]

to produce formulas.