06-1350/Syzygies in Asymptote in Brief
From Drorbn
Jump to navigationJump to search
Installation
See Syzygies in Asymptote for more detailed information.
First install Asymptote. Once installed, download syzygy.asy.
Braids
import syzygy; // Accesses the syzygy module.
Braid b; // Start a new braid.
b.n=3; // The braid has three strands.
// The strands are numbered left to right starting at 0.
b.add(bp,0); // Add a overcrossing component starting at strand 0,
// the leftmost strand.
b.add(bm,1); // Add an undercrossing starting at strand 1.
b.add(phi,0); // Add a trivalent vertex that merges strands 0 and 1.
// Strand 2 is now renumbered as strand 1.
b.draw(); // Draw the resulting braid.
Relations
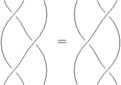
import syzygy; // Access the syzygy module. Braid l; // Define the left hand side of the relation. l.n=3; l.add(bp,0); l.add(bp,1); l.add(bp,0); Braid r; // Define the right hand side of the relation. r.n=3; r.add(bp,1); r.add(bp,0); r.add(bp,1); Relation r3; // Define a relation. r3.lsym="\rho_3"; // Give the relation a name for when it is written in functional form. r3.codename="rho3"; // Give the relation a name to be used by Mathematica. r3.lhs=l; r3.rhs=r; r3.draw();
r3.toFormula() produces the formula:
[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ }[/math]
r3.toLinear() produces the formula in linear form:
[math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3) }[/math]
and r3.toCode() produces a version usable in Mathematica:
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4]
- bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3]
Syzygies
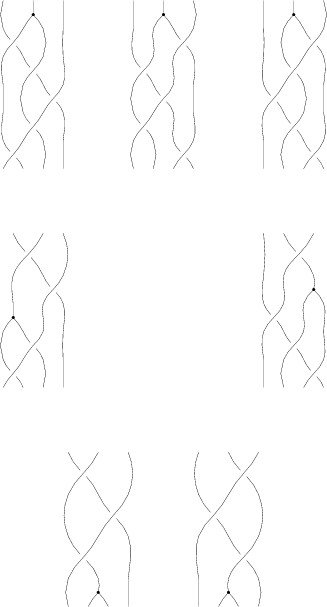
import syzygy; // Phi around B Braid initial; initial.n=4; initial.add(bp,2); initial.add(bp,0); initial.add(bp,1); initial.add(bp,0); initial.add(bp,2); initial.add(phi,1); Syzygy pb; pb.lsym="\Phi B"; pb.codename="PhiAroundB"; pb.initial=initial; pb.apply(r3,1,0); pb.apply(r4a,3,1); pb.swap(2,3); pb.apply(r4b,0,1); pb.apply(-r3,1,0); pb.apply(-r4a,0,0); pb.swap(2,3); pb.apply(-r4b,3,0); pb.apply(r3,1,1); pb.draw();
Again, like relations, we can use pb.toLinear()
| [math]\displaystyle{ \Phi B(x_1,x_2,x_3,x_4,x_5) = }[/math] | [math]\displaystyle{ \rho_3(x_1,x_2,x_3,x_5) + \rho_{4a}(x_1+x_5,x_2,x_3,x_4) + \rho_{4b}(x_1+x_2,x_3,x_4,x_5) }[/math] |
| [math]\displaystyle{ - \rho_3(x_1,x_2,x_3+x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4) }[/math] | |
| [math]\displaystyle{ - \rho_{4b}(x_1,x_3,x_4,x_5) + \rho_3(x_1+x_3,x_2,x_4,x_5). }[/math] |
and pb.toCode()
PhiAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho4a[x1 + x5, x2, x3, x4] + rho4b[x1 + x2, x3, x4, x5] - rho3[x1, x2, x3 + x4, x5] - rho4a[x1, x2, x3, x4] - rho4b[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5]
to produce formulas.