Notes for AKT-140127/0:31:27

Much of this note comes from the paper "Finite type invariants of classical and virtual knots" by Goussarov, Polyak, and Viro, which can be found here: https://arxiv.org/abs/math/9810073. \par

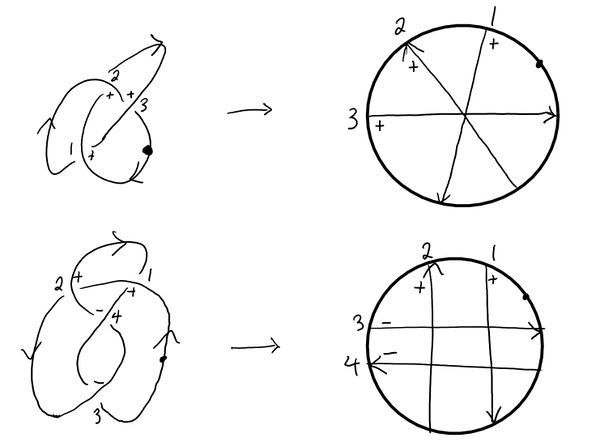
Similar to the process of obtaining an n-chord diagram from an n-singular knot, there is a so called "Gauss diagram" obtainable from a regular knot. I.e. there is a map $\mathcal{K} \rightarrow \mathcal{D}$ from the space of knots into the space of Gauss diagrams. A Gauss diagram is a chord diagram with orientations and signs on the chords. The Gauss diagram of a specific knot is obtained as shown in examples below (the right-handed trefoil and the figure eight knots).

Note the additional information in the Gauss diagram about the overpasses and underpasses of the knot diagram (the orientations on the chords), as well as the sign of the crossings. Unfortunately, unlike the fact that any n-chord diagram is $D_K$ for some n-singular knot $K$, it is not true that any Gauss diagram is the Gauss diagram of a knot. This observation is intimately related to the theory of virtual knots, described in detail in the paper linked above.