User:Drorbn/06-1350-HW4

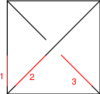
The Generators

Our generators are [math]\displaystyle{ T }[/math], [math]\displaystyle{ R }[/math], [math]\displaystyle{ Y=\Phi }[/math] and [math]\displaystyle{ B^{\pm} }[/math] (we might consider splitting [math]\displaystyle{ Y }[/math] into two, [math]\displaystyle{ Y^{up} }[/math] and [math]\displaystyle{ Y^{dn} }[/math]):

Picture
Generator	[math]\displaystyle{ T }[/math]	[math]\displaystyle{ R }[/math]	[math]\displaystyle{ Y^{up} }[/math]	[math]\displaystyle{ Y^{dn} }[/math]	[math]\displaystyle{ B^+ }[/math]	[math]\displaystyle{ B^- }[/math]
Perturbation	[math]\displaystyle{ t }[/math]	[math]\displaystyle{ r }[/math]	[math]\displaystyle{ y^u }[/math]	[math]\displaystyle{ y^d }[/math]	[math]\displaystyle{ b^+ }[/math]	[math]\displaystyle{ b^- }[/math]

The Relations

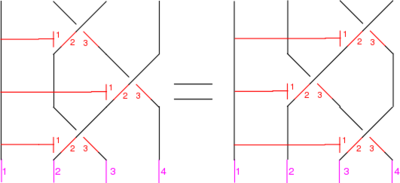
The Reidemeister Move R3

The picture is

In formulas, this is

[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ }[/math].

Thus the R3 component of [math]\displaystyle{ d }[/math] is

[math]\displaystyle{ (1230)^\star b^+ +(1213)^\star b^+ +(1023)^\star b^+ -(1123)^\star b^+ -(1203)^\star b^+ -(1231)^\star b^+ }[/math].