User:Zsuzsi/HW4: Difference between revisions
mNo edit summary |
No edit summary |
||
| Line 36: | Line 36: | ||
[[Image:Reidemeister1.jpg]] |
[[Image:Reidemeister1.jpg]] |
||
We cannot write this in the first notation, as the chords ending on both the second and third red line will end on the second pink line. |
|||
In the linearized functional notation, if I'm getting this right, it looks like this: |
|||
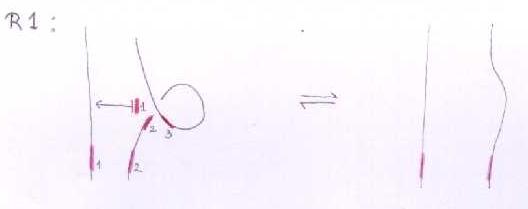
<math> \rho_1(x_1,x_2)=b^-(x_1,x_2,-x_2)</math> |
|||
Where the negative sign is because the order of the chords is reversed as we slide them along the little loop. |
|||
====The Reidemeister move R2==== |
====The Reidemeister move R2==== |
||
With three sides of the shielding removed, the picture is: |
|||
[[Image:Reidemeister2.jpg]] |
[[Image:Reidemeister2.jpg]] |
||
This means: |
|||
<math>(123)^\star B^+ (132)^\star B^- = 1</math> |
|||
Linearized and in functional form: |
|||
<math>\rho_2(x_1,x_2,x_3)=b^+(x_1,x_2,x_3)+b^-(x_1,x_3,x_2) </math> |
|||
((The right side won't contribute anything, right?)) |
|||
====The Reidemeister Move R3==== |
====The Reidemeister Move R3==== |
||
| Line 54: | Line 71: | ||
| |
| |
||
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math> |
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math> |
||
|} |
|||
====The Reidemeister Move R4, source:Andy==== |
|||
First version of R4: |
|||
[[Image:06-1350-R4a.png|center]] |
|||
In formulas, this is |
|||
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star \Phi = (1123)^\star \Phi (1233)^\star B^+</math>.</center> |
|||
Linearized and written in functional form, this becomes |
|||
{| align=center |
|||
|- |
|||
|<math>\rho_{4a}(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + \phi(x_1,x_3,x_4) - \phi(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_3+x_4).</math> |
|||
|} |
|||
Second version: |
|||
[[Image:06-1350-R4b.png|center]] |
|||
In formulas, this is |
|||
<center><math>(1123)^\star B^+ (1203)^\star B^+ (1231)^\star \Phi = (1230)^\star \Phi (1223)^\star B^+</math>.</center> |
|||
Linearized and written in functional form, this becomes |
|||
{| align=center |
|||
|- |
|||
|<math>\rho_{4b}(x_1,x_2,x_3,x_4) = b^+(x_1+x_2,x_3,x_4) + b^+(x_1,x_2,x_4) + \phi(x_1+x_4,x_2,x_3) - \phi(x_1,x_2,x_3) - b^+(x_1,x_2+x_3,x_4).</math> |
|||
|} |
|} |
||
Revision as of 16:43, 4 December 2006
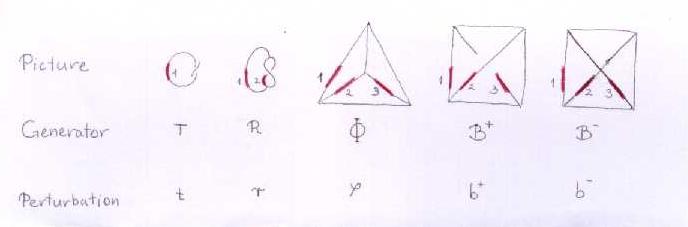
The Generators
Our generators are , , and :
| Picture | 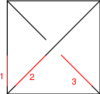
|
||||
| Generator | |||||
| Perturbation |
A low-tech completed version of this chart:
The Relations
The Reidemeister move R1
We cannot write this in the first notation, as the chords ending on both the second and third red line will end on the second pink line.
In the linearized functional notation, if I'm getting this right, it looks like this:
Where the negative sign is because the order of the chords is reversed as we slide them along the little loop.
The Reidemeister move R2
With three sides of the shielding removed, the picture is:
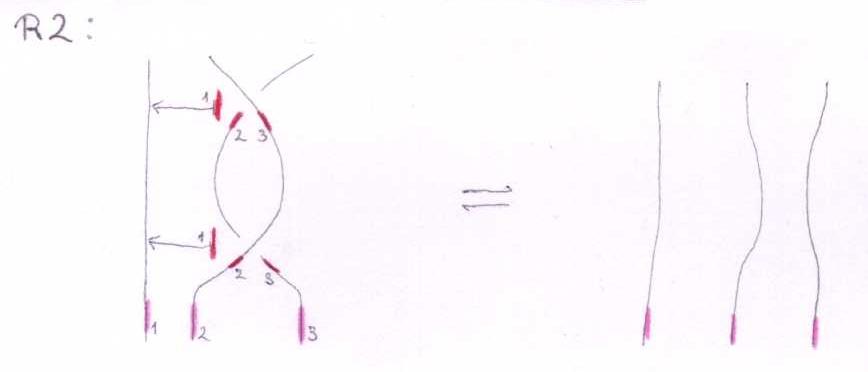
This means:
Linearized and in functional form:
((The right side won't contribute anything, right?))
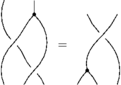
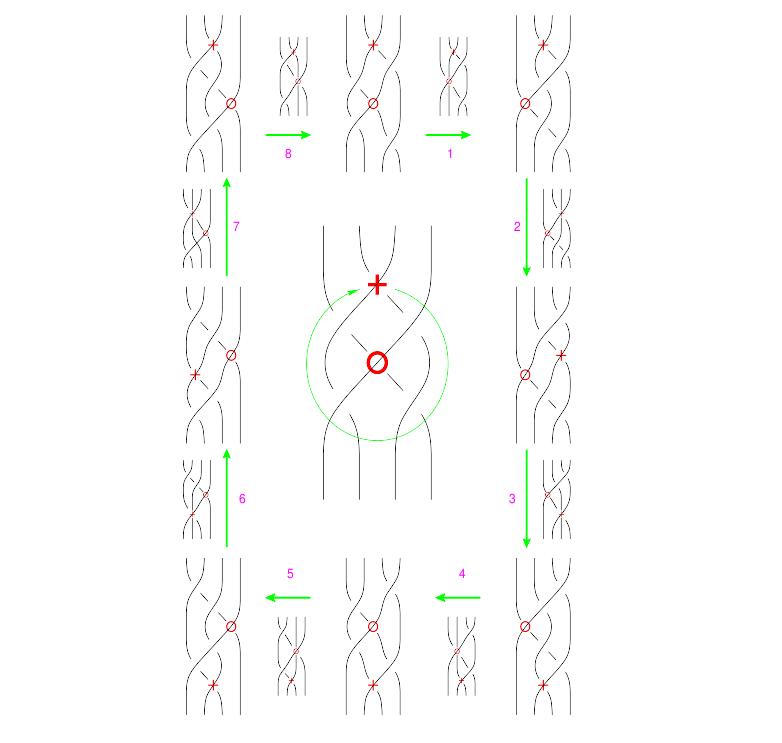
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
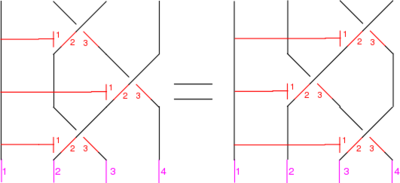
The Reidemeister Move R4, source:Andy
First version of R4:
In formulas, this is
Linearized and written in functional form, this becomes
Second version:
In formulas, this is
Linearized and written in functional form, this becomes
The Syzygies
The "B around B" Syzygy
The picture, with all shielding removed, is
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|