User:Shawkm/06-1350-HW4: Difference between revisions
No edit summary |
No edit summary |
||
| Line 109: | Line 109: | ||
This is probably a completely trivial remark, and it is also trivial to see that mathematica will deal with this in the same way as for <math> b^+ </math> so I won't verify that <math> d^2 =0 </math>. |
This is probably a completely trivial remark, and it is also trivial to see that mathematica will deal with this in the same way as for <math> b^+ </math> so I won't verify that <math> d^2 =0 </math>. |
||
What I will do now is linearize and write down in functional form the relation R2 |
|||
{| align=center |
|||
|- |
|||
|<math>\rho_2(x_1, x_2, x_3) = </math> |
|||
|<math>b^+(x_1,x_2,x_3) + b^-(x_1,x_3,x_2)</math> |
|||
|} |
|||
or |
|||
{| align=center |
|||
|- |
|||
|<math>\rho_2(x_1, x_2, x_3) = </math> |
|||
|<math>b^-(x_1,x_2,x_3) + b^+(x_1,x_3,x_2)</math> |
|||
|} |
|||
Revision as of 19:34, 2 December 2006
The Generators
Our generators are , , and :
| Picture | 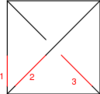
|
||||
| Generator | |||||
| Perturbation |
The Relations
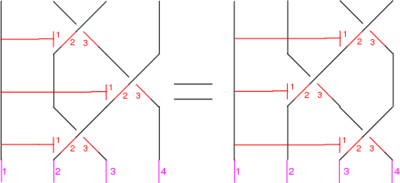
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
The Syzygies
The "B around B" Syzygy
The picture, with all shielding removed, is
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|
Here Goes Something New(?)
The first thing to notice is that the relation holds for and so we have another version:
This is probably a completely trivial remark, and it is also trivial to see that mathematica will deal with this in the same way as for so I won't verify that .
What I will do now is linearize and write down in functional form the relation R2
or