User:Drorbn/06-1350-HW4: Difference between revisions

From Drorbn
Jump to navigationJump to search
No edit summary
No edit summary
Line 1: Line 1:
===The Generators===
===The Generators===


Our generators are <math>T</math>, <math>R</math>, <math>Y=\Phi</math> and <math>B^{\pm}</math> (we might consider splitting <math>Y</math> into two, <math>Y^{up}</math> and <math>Y^{dn}</math>):
Our generators are <math>T</math>, <math>R</math>, <math>\Phi</math> and <math>B^{\pm}</math>:
{| align=center
{| align=center cellpadding=10 style="border: solid orange 1px"
|- align=center valign=middle
|- align=center valign=middle
|align=left|Picture
|align=left|Picture
⚫
|
|
|
|
|
Line 15: Line 14:
|<math>T</math>
|<math>T</math>
|<math>R</math>
|<math>R</math>
|<math>Y^{up}</math>
|<math>\Phi</math>
|<math>Y^{dn}</math>
|<math>B^+</math>
|<math>B^+</math>
|<math>B^-</math>
|<math>B^-</math>
Line 23: Line 21:
|<math>t</math>
|<math>t</math>
|<math>r</math>
|<math>r</math>
|<math>y^u</math>
|<math>\varphi</math>
|<math>y^d</math>
|<math>b^+</math>
|<math>b^+</math>
|<math>b^-</math>
|<math>b^-</math>
Line 36: Line 33:
In formulas, this is
In formulas, this is
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+</math>.</center>
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+</math>.</center>
Linearized and written in functional form, this becomes
Thus the R3 component of <math>d</math> is
{| align=center
<center><math>(1230)^\star b^+ +(1213)^\star b^+ +(1023)^\star b^+ -(1123)^\star b^+ -(1203)^\star b^+ -(1231)^\star b^+</math>.</center>
|-
|<math>\rho_3(x_1, x_2, x_3, x_4) = </math>
|<math>b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)</math>
|-
⚫
|
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math>
|}


===The Syzygies===
===The Syzygies===

Revision as of 17:38, 18 November 2006

The Generators

Our generators are [math]\displaystyle{ T }[/math], [math]\displaystyle{ R }[/math], [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ B^{\pm} }[/math]:

Picture 06-1350-BPlus.svg
Generator [math]\displaystyle{ T }[/math] [math]\displaystyle{ R }[/math] [math]\displaystyle{ \Phi }[/math] [math]\displaystyle{ B^+ }[/math] [math]\displaystyle{ B^- }[/math]
Perturbation [math]\displaystyle{ t }[/math] [math]\displaystyle{ r }[/math] [math]\displaystyle{ \varphi }[/math] [math]\displaystyle{ b^+ }[/math] [math]\displaystyle{ b^- }[/math]

The Relations

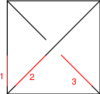
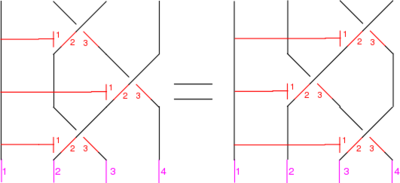
The Reidemeister Move R3

The picture is

06-1350-R4.svg

In formulas, this is

[math]\displaystyle{ (1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+ }[/math].

Linearized and written in functional form, this becomes

[math]\displaystyle{ \rho_3(x_1, x_2, x_3, x_4) = }[/math] [math]\displaystyle{ b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) }[/math]
[math]\displaystyle{ - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3). }[/math]

The Syzygies

A Mathematica Verification

Retrieved from "https://drorbn.net/index.php?title=User:Drorbn/06-1350-HW4&oldid=2813"