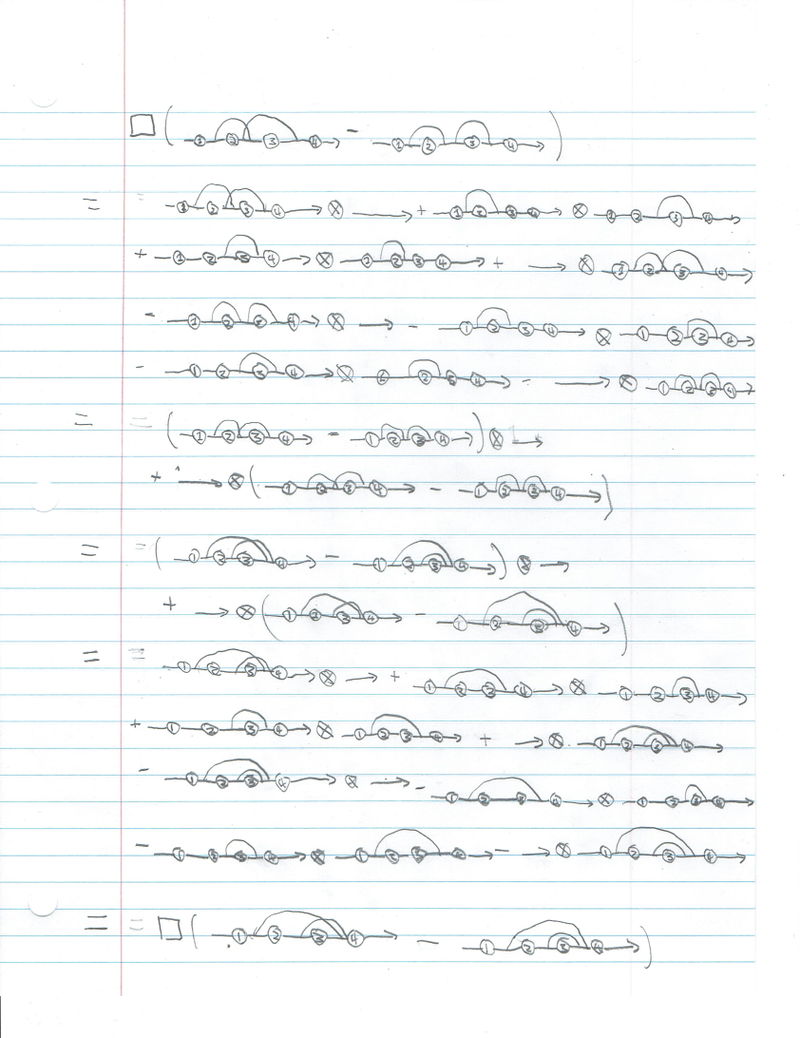Notes for AKT-140324/0:51:37: Difference between revisions
From Drorbn
Jump to navigationJump to search
Gavin.hurd (talk | contribs) (Created page with "Showing that the box coproduct respects the 4T relation. Throughout, the tensor of two diagrams actually refers to a sum of all possible ways of placing the connected compone...") |
Gavin.hurd (talk | contribs) No edit summary |
||
| Line 1: | Line 1: | ||
Showing that the box coproduct respects the 4T relation. |
Showing that the box coproduct respects the 4T relation. |
||
Throughout, the tensor of two diagrams actually refers to a sum of all possible ways of placing the connected components of the sub-diagrams 1, 2, 3, and 4 on the left or right side of the tensor, in line with the definition of box. |
Throughout, the tensor of two diagrams actually refers to a sum of all possible ways of placing the connected components of the sub-diagrams 1, 2, 3, and 4 on the left or right side of the tensor, in line with the definition of box. |
||
[[File:Box with 4T-1.jpg]] |
[[File:Box with 4T-1.jpg|800px]] |
||
Latest revision as of 22:33, 8 August 2018
Showing that the box coproduct respects the 4T relation.
Throughout, the tensor of two diagrams actually refers to a sum of all possible ways of placing the connected components of the sub-diagrams 1, 2, 3, and 4 on the left or right side of the tensor, in line with the definition of box.
