User:Zak/06-1350-HW4

Disclaimer

This page has nothing new yet! I've just copied Dror's page. If this page can't be smart maybe it can look good. I've made some SVG files of the generators mimicking Dror's BPlus. Feel free to copy them so I don't feel bad about copying you.

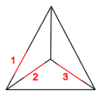
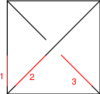
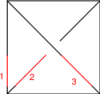
The Generators

Our generators are $T$, $R$, $\Phi$ and $B^{\pm }$:

Picture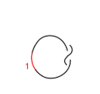
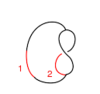
Generator	$T$	$R$	$\Phi$	$B^{+}$	$B^{-}$
Perturbation	$t$	$r$	$\varphi$	$b^{+}$	$b^{-}$

The Relations

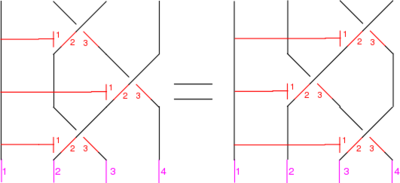
The Reidemeister Move R3

The picture (with three sides of the shielding removed) is

In formulas, this is

$(1230)^{\star }B^{+}(1213)^{\star }B^{+}(1023)^{\star }B^{+}=(1123)^{\star }B^{+}(1203)^{\star }B^{+}(1231)^{\star }B^{+}$.

Linearized and written in functional form, this becomes

$\rho _{3}(x_{1},x_{2},x_{3},x_{4})=$	$b^{+}(x_{1},x_{2},x_{3})+b^{+}(x_{1}+x_{3},x_{2},x_{4})+b^{+}(x_{1},x_{3},x_{4})$
	$-b^{+}(x_{1}+x_{2},x_{3},x_{4})-b^{+}(x_{1},x_{2},x_{4})-b^{+}(x_{1}+x_{4},x_{2},x_{3}).$

The Syzygies

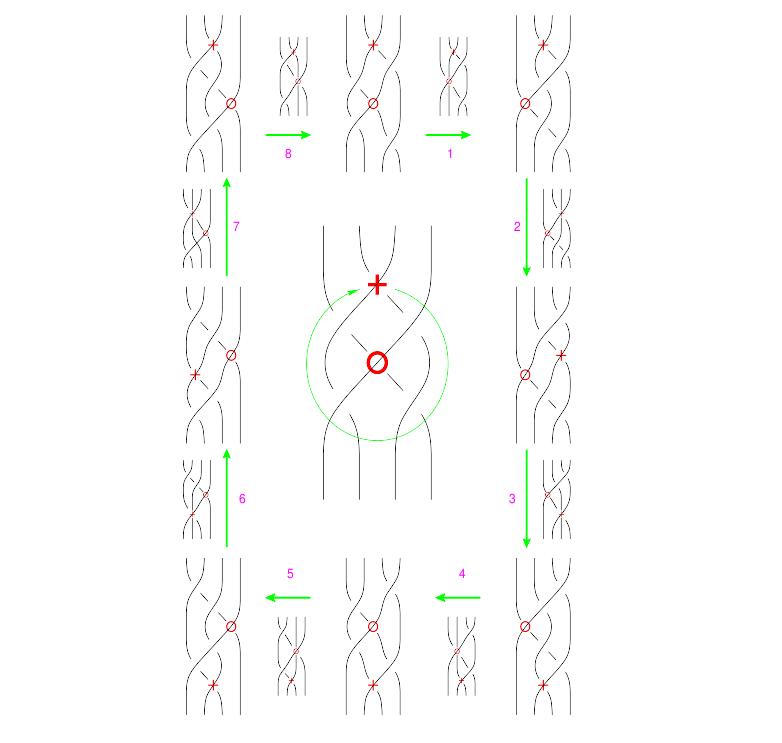
The "B around B" Syzygy

The picture, with all shielding removed, is

(Drawn with Inkscape) (note that lower quality pictures are also acceptable)

The functional form of this syzygy is

$BB(x_{1},x_{2},x_{3},x_{4},x_{5})=$	$\rho _{3}(x_{1},x_{2},x_{3},x_{5})+\rho _{3}(x_{1}+x_{5},x_{2},x_{3},x_{4})-\rho _{3}(x_{1}+x_{2},x_{3},x_{4},x_{5})$
	$-\rho _{3}(x_{1},x_{2},x_{4},x_{5})-\rho _{3}(x_{1}+x_{4},x_{2},x_{3},x_{5})-\rho _{3}(x_{1},x_{2},x_{3},x_{4})$
	$+\rho _{3}(x_{1},x_{3},x_{4},x_{5})+\rho _{3}(x_{1}+x_{3},x_{2},x_{4},x_{5}).$

A Mathematica Verification

The following simulated Mathematica session proves that for our single relation and single syzygy, $d^{2}=0$. Copy paste it into a live Mathematica session to see that it's right!

In[1]:=

d1 = { rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] }; d2 = { BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] };

In[3]:=	BAroundB[x1, x2, x3, x4, x5] /. d2
Out[3]=	- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] + rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4]

In[4]:=	BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
Out[4]=	0