User:Drorbn/06-1350-HW4: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
|||
| (10 intermediate revisions by the same user not shown) | |||
| Line 29: | Line 29: | ||
====The Reidemeister Move R3==== |
====The Reidemeister Move R3==== |
||
The picture is |
The picture (with three sides of the shielding removed) is |
||
[[Image:06-1350-R4.svg|400px|center]] |
[[Image:06-1350-R4.svg|400px|center]] |
||
In formulas, this is |
In formulas, this is |
||
| Line 44: | Line 44: | ||
===The Syzygies=== |
===The Syzygies=== |
||
====The "B around B" Syzygy==== |
|||
The picture, with all shielding removed, is |
|||
{| align=center |
|||
|- align=center |
|||
|[[Image:06-1350-BAroundB.svg|center]] |
|||
|- |
|||
|align=right|(Drawn with [http://www.inkscape.org/ Inkscape])<br>(note that lower quality pictures are also acceptable) |
|||
|} |
|||
The functional form of this syzygy is |
|||
{| align=center |
|||
|- |
|||
|<math>BB(x_1,x_2,x_3,x_4,x_5) = </math> |
|||
|<math>\rho_3(x_1, x_2, x_3, x_5) + \rho_3(x_1 + x_5, x_2, x_3, x_4) - \rho_3(x_1 + x_2, x_3, x_4, x_5)</math> |
|||
|- |
|||
| |
|||
|<math>- \rho_3(x_1, x_2, x_4, x_5) - \rho_3(x_1 + x_4, x_2, x_3, x_5) - \rho_3(x_1, x_2, x_3, x_4)</math> |
|||
|- |
|||
| |
|||
|<math>+ \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5).</math> |
|||
|} |
|||
===A Mathematica Verification=== |
===A Mathematica Verification=== |
||
The following simulated Mathematica session proves that for our single relation and single syzygy, <math>d^2=0</math>. Copy paste it into a live Mathematica session to see that it's right! |
|||
{{In|n=1|in=<nowiki>d1 = { |
|||
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + |
|||
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - |
|||
bp[x1 + x4, x2, x3] |
|||
}; |
|||
d2 = { |
|||
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + |
|||
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - |
|||
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - |
|||
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + |
|||
rho3[x1 + x3, x2, x4, x5] |
|||
};</nowiki>}} |
|||
{{InOut|n=3|in=<nowiki>BAroundB[x1, x2, x3, x4, x5] /. d2</nowiki>|out=<nowiki>- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] |
|||
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] |
|||
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] |
|||
+ rho3[x1 + x5, x2, x3, x4]</nowiki>}} |
|||
{{InOut|n=4|in=<nowiki>BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1</nowiki>|out=<nowiki>0</nowiki>}} |
|||
Latest revision as of 18:41, 20 November 2006
The Generators
Our generators are [math]\displaystyle{ T }[/math], [math]\displaystyle{ R }[/math], [math]\displaystyle{ \Phi }[/math] and [math]\displaystyle{ B^{\pm} }[/math]:
The Relations
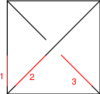
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
| [math]\displaystyle{ \rho_3(x_1, x_2, x_3, x_4) = }[/math] | [math]\displaystyle{ b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4) }[/math] |
| [math]\displaystyle{ - b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3). }[/math] |
The Syzygies
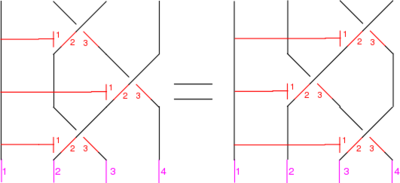
The "B around B" Syzygy
The picture, with all shielding removed, is
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
| [math]\displaystyle{ BB(x_1,x_2,x_3,x_4,x_5) = }[/math] | [math]\displaystyle{ \rho_3(x_1, x_2, x_3, x_5) + \rho_3(x_1 + x_5, x_2, x_3, x_4) - \rho_3(x_1 + x_2, x_3, x_4, x_5) }[/math] |
| [math]\displaystyle{ - \rho_3(x_1, x_2, x_4, x_5) - \rho_3(x_1 + x_4, x_2, x_3, x_5) - \rho_3(x_1, x_2, x_3, x_4) }[/math] | |
| [math]\displaystyle{ + \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5). }[/math] |
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, [math]\displaystyle{ d^2=0 }[/math]. Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|