Notes for AKT-140310/0:35:45: Difference between revisions
No edit summary |
No edit summary |
||
| (3 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
In this note, we compute and interpret the structure constants $f_{abc}$ of $so(N)$, as well as the two-index tensors $t_{ab}$ encoding the information from the metric. In other words, we follow a similar process to the lecture, while disregarding the representation/skeleton edges. |
In this note, we compute and interpret the structure constants $f_{abc}$ of $so(N)$, as well as the two-index tensors $t_{ab}$ encoding the information from the metric. In other words, we follow a similar process to the lecture, while disregarding the representation/skeleton edges. |
||
Let $so(N) = \{Q \in gl(N) | Q^TQ = QQ^T = I, |
Let $so(N) = \{Q \in gl(N) | Q^TQ = QQ^T = I, detQ = 1\}$, with the commutator as its bracket (i.e. $[A,B] = AB - BA$), and the metric $\langle A, B \rangle = tr(AB)$. |
||
Let $\{\pm M_{ij}\}_{i < j}$ be a basis for $so(N)$, where $(M_{ij})_{kl} = \delta_{ij}\delta_{jl} - \delta_{il}\delta_{jk}$. |
Let $\{\pm M_{ij}\}_{i < j}$ be a basis for $so(N)$, where $(M_{ij})_{kl} = \delta_{ij}\delta_{jl} - \delta_{il}\delta_{jk}$. |
||
Latest revision as of 14:20, 8 August 2018
In this note, we compute and interpret the structure constants $f_{abc}$ of $so(N)$, as well as the two-index tensors $t_{ab}$ encoding the information from the metric. In other words, we follow a similar process to the lecture, while disregarding the representation/skeleton edges.
Let $so(N) = \{Q \in gl(N) | Q^TQ = QQ^T = I, detQ = 1\}$, with the commutator as its bracket (i.e. $[A,B] = AB - BA$), and the metric $\langle A, B \rangle = tr(AB)$.
Let $\{\pm M_{ij}\}_{i < j}$ be a basis for $so(N)$, where $(M_{ij})_{kl} = \delta_{ij}\delta_{jl} - \delta_{il}\delta_{jk}$.
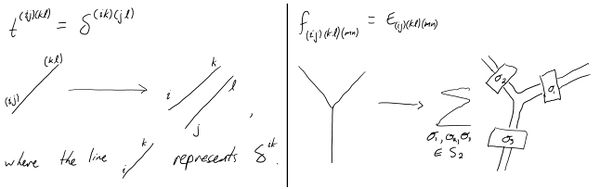
With this, compute $$t_{(ij)(kl)} = \langle M_{ij}, M_{kl} \rangle = tr(M_{ij}M_{kl}) = const\cdot\delta_{ik}\delta_{jl}$$
Note that this also gives us the inverses $t^{(ij)(kl)} = const\cdot\delta^{ik}\delta^{jl}$.
Now the structure constants: $$f_{(ij)(kl)(mn)} = \langle[M_{ij}, M_{kl}], M_{mn} \rangle = \langle M_{ij}M_{kl}, M_{mn} \rangle - \langle M_{kl}M_{ij}, M_{mn} \rangle$$ $$f_{(ij)(kl(mn)} = tr(M_{ij}M_{kl}M_{mn}) - tr(M_{kl}M_{ij}M_{mn}) = const\cdot\epsilon_{(ij)(kl)(mn)}$$
(With an appropriate choice of signs and ordering of the basis. In $so(3)$, an appropriate ordering and choice of signs is $\mathcal{B} = \{M_{12}, M_{23}, -M_{13}\}$.
If we order the basis, we can associate an integer lying somewhere from 1 to $N(N-1)/2$ (the dimension of $so(N)$) to each pair of indices $(ij)$, so the expression $\epsilon_{(ij)(kl)(mn)}$ makes sense - namely, let $a$, $b$, and $c$ correspond to $(ij)$, $(kl)$, and $(mn)$, respectively, and let $\epsilon_{(ij)(kl)(mn)} = \epsilon_{abc}$, the usual totally antisymmetric tensor.
Thus, up to a constant, $t^{(ij)(kl)} = \delta^{ik}\delta^{jl}$ and $f_{(ij)(kl)(mn)} = \epsilon_{(ij)(kl)(mn)}$.
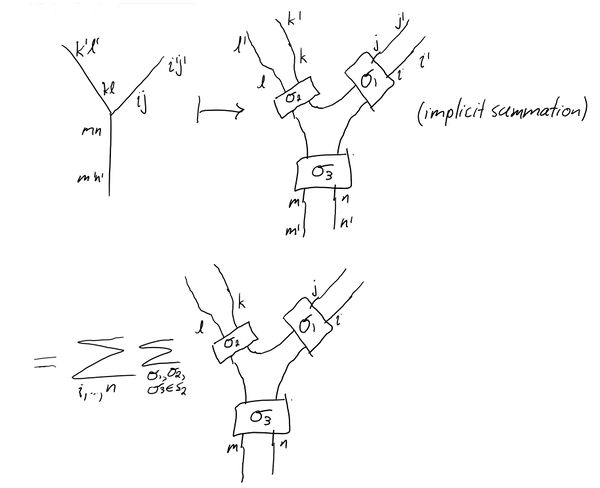
As in the $gl(N)$ case, we can represent the result $t^{(ij)(kl)} = \delta^{ik}\delta^{jl}$ as a splitting of two lines in the diagram, as in the image below. In addition, we can represent the result $f_{(ij)(kl)(mn)} = \epsilon_{(ij)(kl)(mn)}$ as a trivalent vertex becoming a sum of diagrams, over transpositions of certain lines.
The diagram illustrated below goes to the following expression: $$I = \sum_{i,...,n,i',...,n'}f_{(ij)(kl)(mn)}t^{(ij)(i'j')}t^{(kl)(k'l')}t^{(mn)(m'n')}$$ $$I = \sum_{i,...,n,i',...,n'}\epsilon_{(ij)(kl)(mn)}\delta^{ii'}\delta^{jj'}\delta^{kk'}\delta^{ll'}\delta^{mm'}\delta^{nn'}$$ $$I = \sum_{i,...,n}\epsilon_{(ij)(kl)(mn)}$$
The last line exactly corresponds with the last illustration.