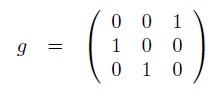11-1100/MATLAB Code for Non-Commutative Gaussian Elimination: Difference between revisions
No edit summary |
m (MATLAB Code for Non-Commutative Gaussian Elimination moved to 11-1100/MATLAB Code for Non-Commutative Gaussian Elimination) |
||
| (9 intermediate revisions by one other user not shown) | |||
| Line 5: | Line 5: | ||
[[Image:Matrix.jpg]] |
[[Image:Matrix.jpg]] |
||
From a computational standpoint this is kind of a bad idea, but I figured it was something different and no one else was likely to try this. |
From a computational standpoint this is kind of a bad idea, but I figured it was something different and no one else was likely to try this solution. |
||
First, I needed to define the problem for the computer. I picked an enumeration of the faces of the 2x2x2 cube, and wrote out the generators of the group based on this enumeration. The rotations of the faces are the generators for the group operations. Since the cube has six faces which can be rotated, there are six generators. The group I am dealing with is a subgroup of the permutations on 24 elements because a 2x2x2 cube has 6*4 = 24 faces. The following figure shows how I chose my enumeration of the cube faces: |
|||
I split the program into 3 parts: BG2.m is a short script which |
|||
[[Image:cubelayout.jpg]] |
|||
(A) This sub-figure demonstrates the enumeration of the faces that I adopted. (B) An image of the Pocket Cube. (C) A list of the group generators (face rotations). |
|||
Note that since the pocket cube has no faces which would fix its overall orientation, there are actually 24 equivalent cube configurations per permutation; thus, whatever answer is obtained at the end needs to be divided by 24 to give the actual group order. |
|||
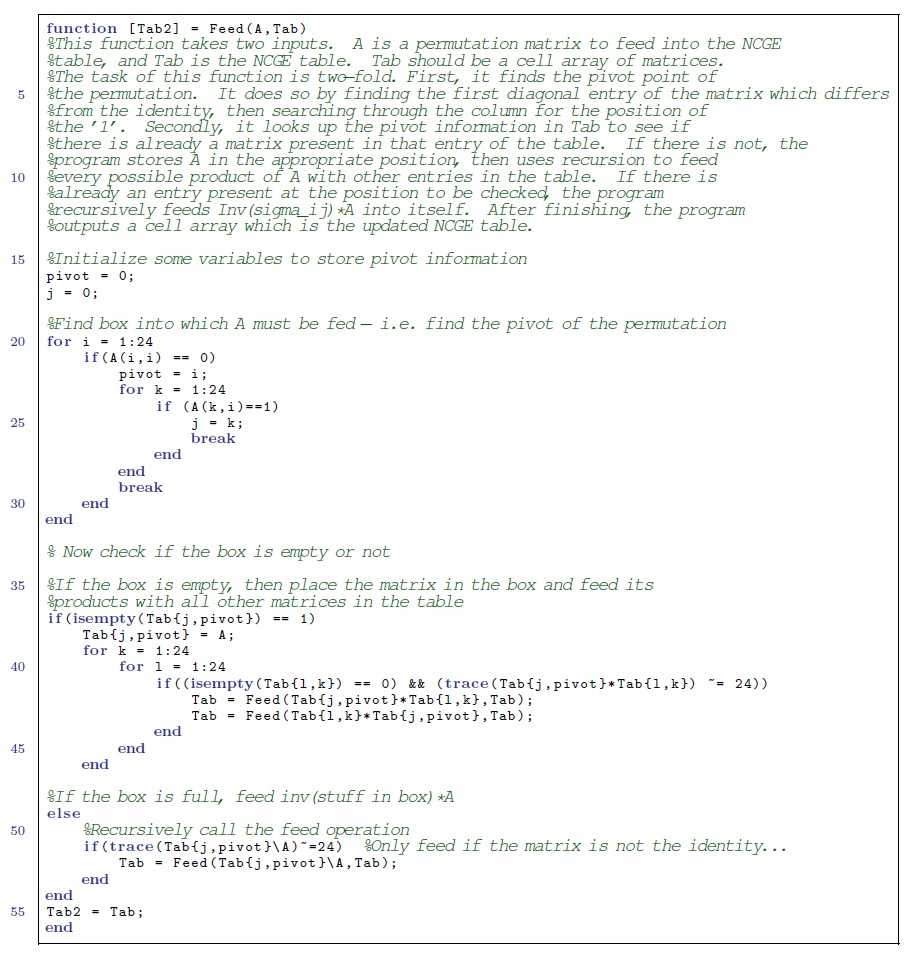
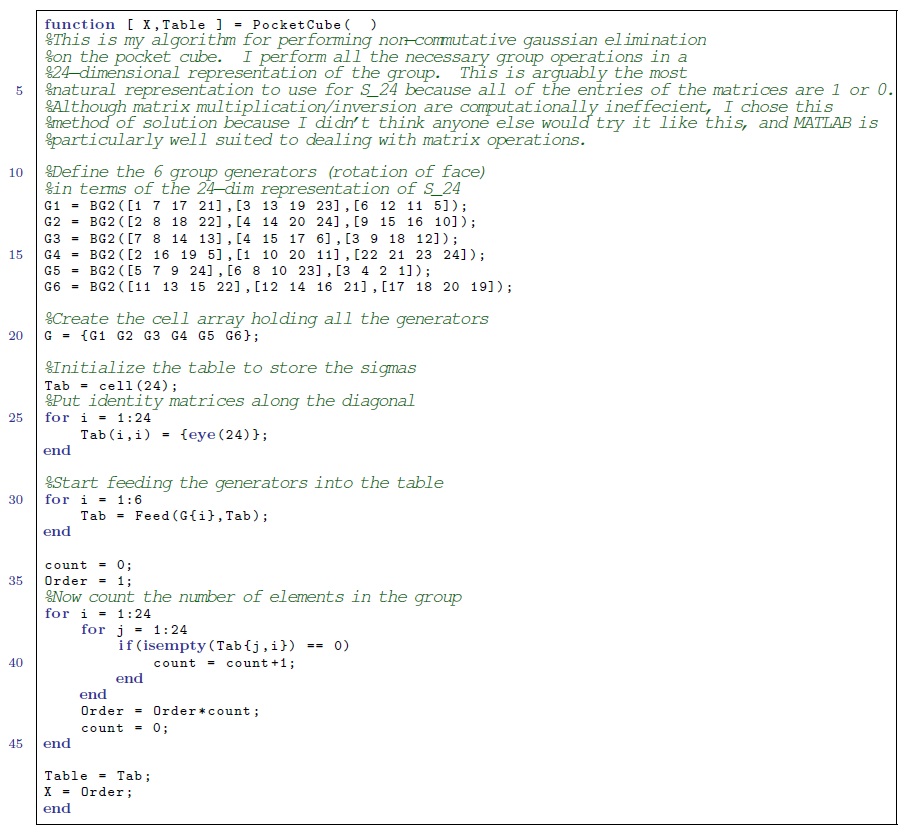
I split the program into 3 parts. BG2.m is a short script which builds the matrix representations of the generators. Feed.m is a script which carries out the non-commutative Gaussian elimination algorithm. Finally, PocketCube.m is a parent script in which the generators of the pocket cube problem are defined, the Feed algorithm is called for each generator, and once the lookup table is finally constructed, the order of the group is output. |
|||
[[Image:BG2.jpg]] |
[[Image:BG2.jpg]] |
||
[[Image:Feed.jpg]] |
[[Image:Feed.jpg]] |
||
[[Image:PocketCube.jpg]] |
[[Image:PocketCube.jpg]] |
||
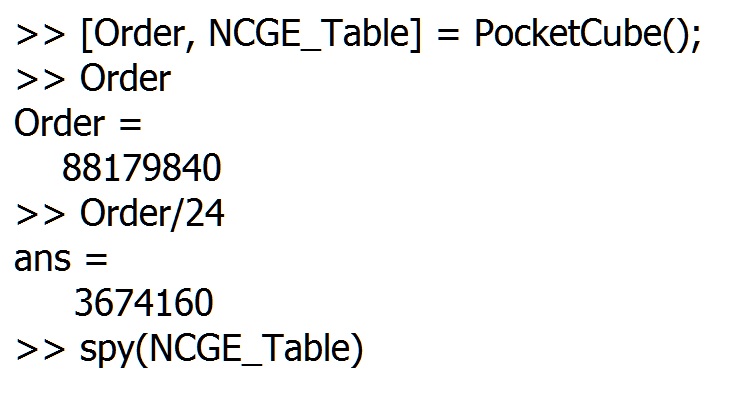
At the MATLAB prompt, the following set of commands were used to run my program: |
|||
[[Image:output.jpg]] |
|||
[[Image:pivot.jpg]] |
|||
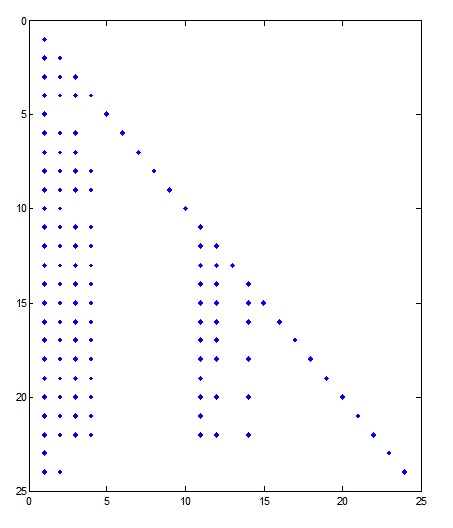
The above plot is displaying the non-zero entries in the NCGE table. I calculate the order of the Pocket Cube group to be 3,674,160. I also ran the program using a restricted subset of the generators. Interestingly, the entire pocket cube group can be generated using only 3 of the face rotations! |
|||
Latest revision as of 17:36, 10 October 2011
I wrote a MATLAB script to carry out the non-commutative Gaussian elimination algorithm. Specifically, I have chosen to use the problem of the 2x2x2 pocket cube; however, this algorithm may be easily adapted for finding the solution to other combinatorial puzzles. The structure of the script is very similar to Dror's code. I call the "Feed" script for each generator of the puzzle, but the built in recursion takes care of finding an empty spot in the table, as well as all the messiness of feeding all products of everything in the table.
My solution is slightly different, however, in that I carry out group operations using matrix representations of the generators. I picked a representation of the group in which every matrix was comprised of only 1's and 0's. This is useful, because it easily allows me to compute products, inverses, and find pivot points. The representation of which I write can be constructed by considering the action of [math]\displaystyle{ S_{n} }[/math] on an n-dimensional vector space. As an example, consider the permutation [math]\displaystyle{ g = (1 2 3) \in S_{3} }[/math]. This permutation takes 1 -> 2, 2 -> 3, and 3 -> 1; thus, the matrix representation of this operation is:
From a computational standpoint this is kind of a bad idea, but I figured it was something different and no one else was likely to try this solution.
First, I needed to define the problem for the computer. I picked an enumeration of the faces of the 2x2x2 cube, and wrote out the generators of the group based on this enumeration. The rotations of the faces are the generators for the group operations. Since the cube has six faces which can be rotated, there are six generators. The group I am dealing with is a subgroup of the permutations on 24 elements because a 2x2x2 cube has 6*4 = 24 faces. The following figure shows how I chose my enumeration of the cube faces:
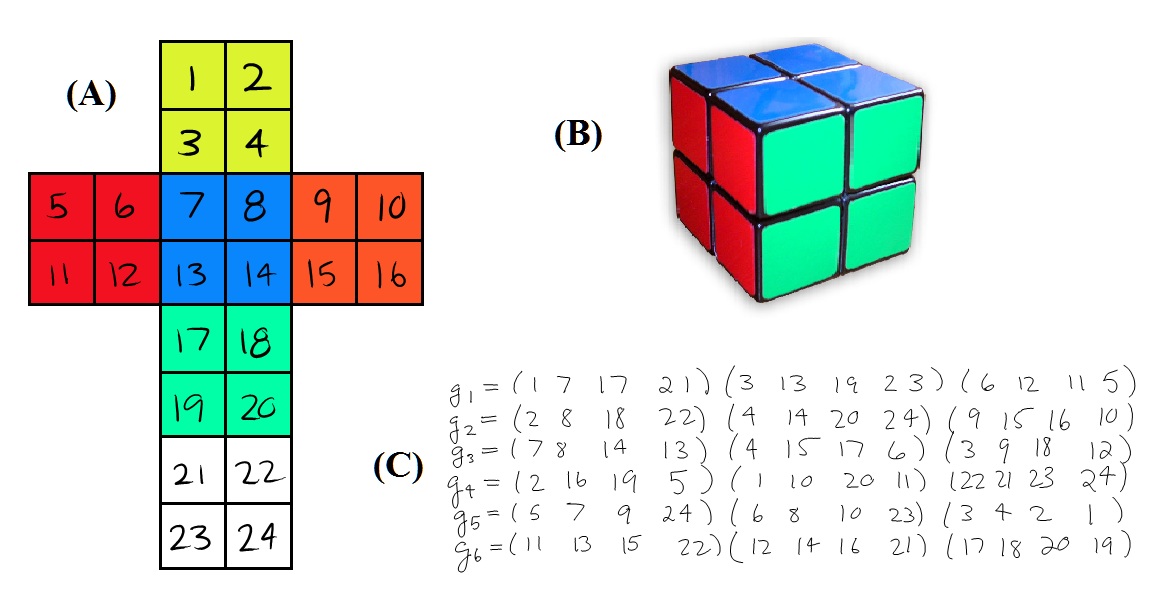 (A) This sub-figure demonstrates the enumeration of the faces that I adopted. (B) An image of the Pocket Cube. (C) A list of the group generators (face rotations).
(A) This sub-figure demonstrates the enumeration of the faces that I adopted. (B) An image of the Pocket Cube. (C) A list of the group generators (face rotations).
Note that since the pocket cube has no faces which would fix its overall orientation, there are actually 24 equivalent cube configurations per permutation; thus, whatever answer is obtained at the end needs to be divided by 24 to give the actual group order.
I split the program into 3 parts. BG2.m is a short script which builds the matrix representations of the generators. Feed.m is a script which carries out the non-commutative Gaussian elimination algorithm. Finally, PocketCube.m is a parent script in which the generators of the pocket cube problem are defined, the Feed algorithm is called for each generator, and once the lookup table is finally constructed, the order of the group is output.
At the MATLAB prompt, the following set of commands were used to run my program:
The above plot is displaying the non-zero entries in the NCGE table. I calculate the order of the Pocket Cube group to be 3,674,160. I also ran the program using a restricted subset of the generators. Interestingly, the entire pocket cube group can be generated using only 3 of the face rotations!