09-240/Classnotes for Tuesday December 1: Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| Line 23: | Line 23: | ||
* Also, note that exchanging two rows flips the sign. |
* Also, note that exchanging two rows flips the sign. |
||
2. <math>det(E^2_{i,c\,\!}A) = det(A) ; | |
2. <math>det(E^2_{i,c\,\!}A) = det(A) ; |E^2_{i,j,c\,\!}| = 1</math> |
||
* These are "enough"! |
* These are "enough"! |
||
3. <math>det((E_{i,j,c\,\!}A) = det(A) ; | |
3. <math>det((E_{i,j,c\,\!}A) = det(A) ; |E^3_{i,j,c\,\!}| = 1</math> |
||
* Adding a multiple of one row to another does not change the determinant. |
* Adding a multiple of one row to another does not change the determinant. |
||
| Line 34: | Line 34: | ||
<b>Theorem:</b> |
<b>Theorem:</b> |
||
If <math> det' : M_{nxn\,\!}</math>→F satisfies properties 0-3 above, then <math>det' = det</math> |
|||
<math>det(A) = det'(A)</math> |
|||
Philosophical remark: Why not begin our inquiry with the properties above? |
|||
We must find an implied need for their use; thus, we must know whether a function <math>det</math> exists first. |
|||
Revision as of 16:31, 1 December 2009
--- Wiki Format ---
MAT240 – December 1st
Basic Properties of det: Mnxn→F: 0 det(I) = 1
1.
- Also, note that exchanging two rows flips the sign.
2.
- These are "enough"!
3.
- Adding a multiple of one row to another does not change the determinant.
The determinant of any matrix can be calculated using the properties above.
Theorem:
If →F satisfies properties 0-3 above, then
Philosophical remark: Why not begin our inquiry with the properties above?
We must find an implied need for their use; thus, we must know whether a function exists first.


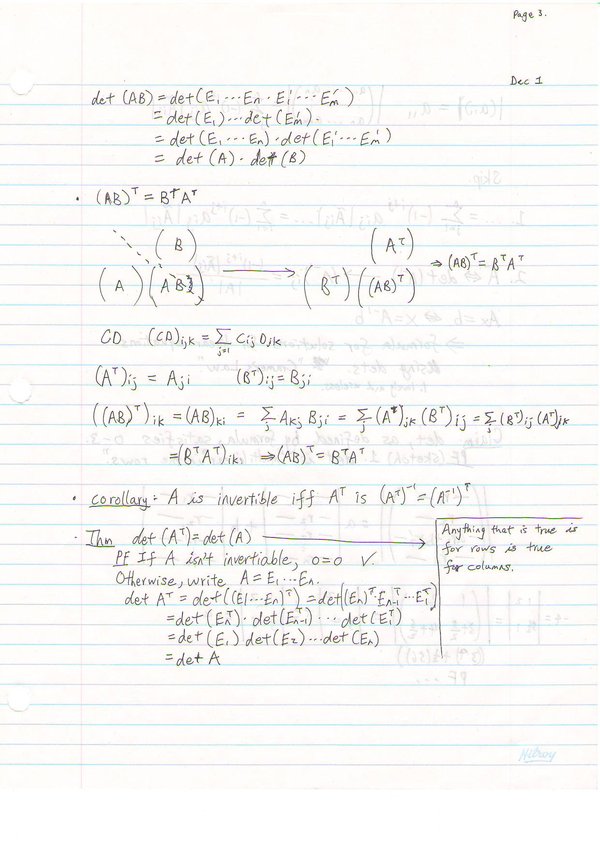
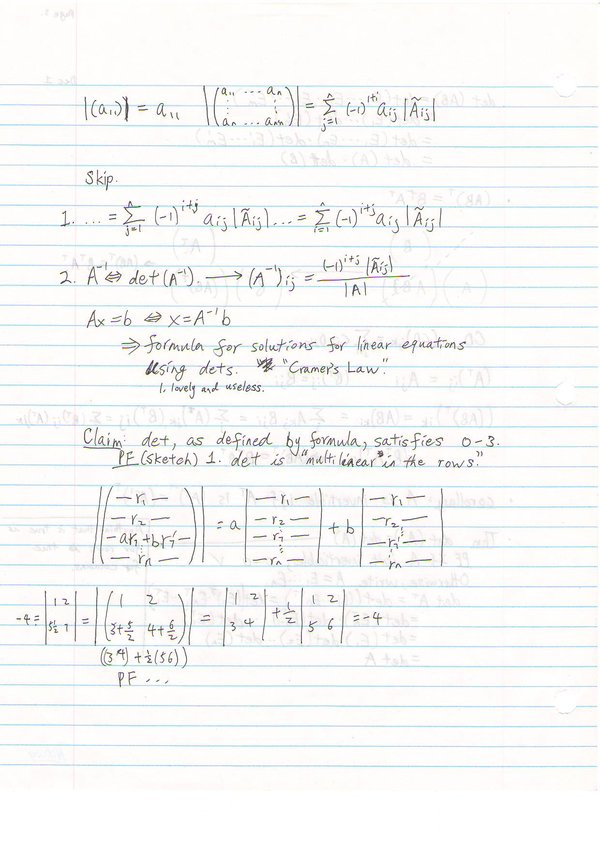
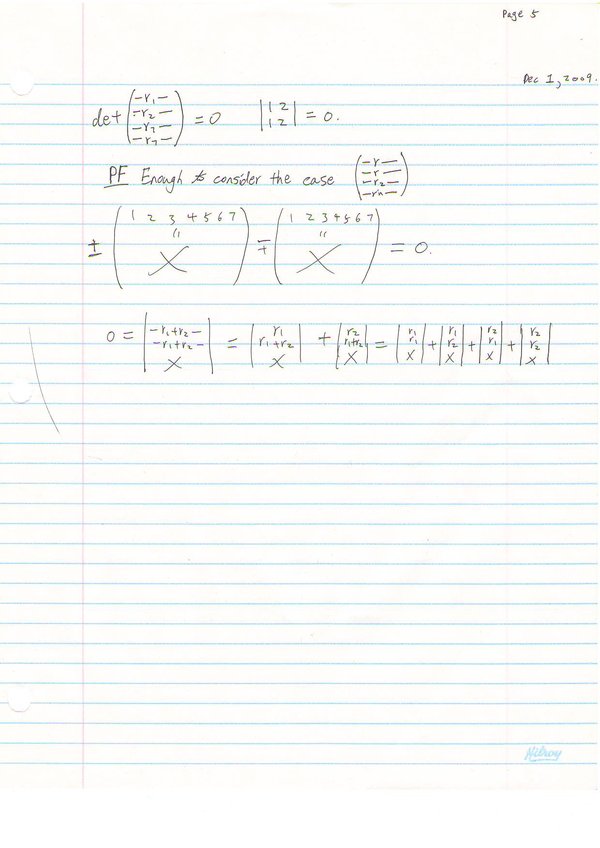




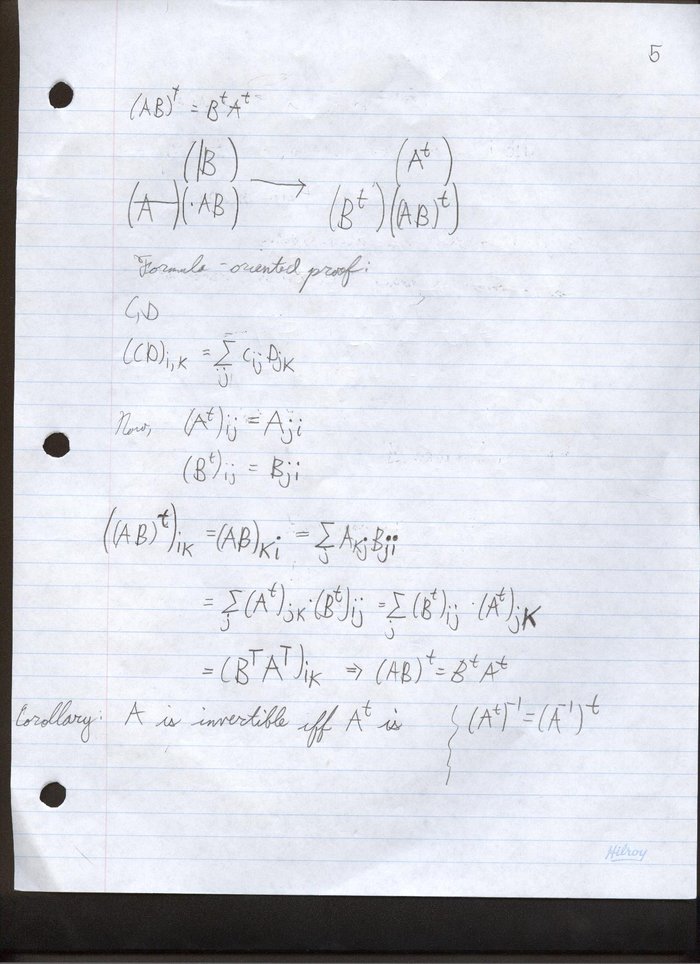



![{\displaystyle det(E'_{i,j\,\!}A)=-det(A);|E'_{i,j\,\!}|=-1.[Note:det(EA)=|E||A|]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/93b201c57138463bb97bc0ea059970a95c7d0fd0)





