07-401/Homework Assignment 10 (and last!): Difference between revisions
From Drorbn
Jump to navigationJump to search
No edit summary |
No edit summary |
||
| (4 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
{{07-401/Navigation}} |
{{07-401/Navigation}} |
||
{{In Preparation}} |
|||
===Reading=== |
===Reading=== |
||
| Line 9: | Line 8: | ||
===Doing=== |
===Doing=== |
||
Solve problems |
Solve problems 1, 4, 6#, 8#, 14#, 15#, 16 and 18 in Chapter 32 of Gallian's book but submit only the solutions of the problems marked with a sharp (#). |
||
===Due Date=== |
===Due Date=== |
||
This assignment is due in class on Wednesday April 11, 2007. |
This assignment is due in class on Wednesday April 11, 2007. |
||
===Just for Fun=== |
|||
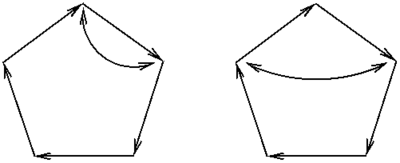
'''1.''' Prove that the following two "pentagonal rubik's style" combinatorial games are always solvable: |
|||
[[Image:07-401-Pentagon Games.png|center|400px]] |
|||
'''2.''' Which of the following three "hexagonal rubik's style" combinatorial games are always solvable? |
|||
[[Image:07-401-Hexagon Games.png|center|480px]] |
|||
Latest revision as of 20:19, 4 April 2007
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Reading
Read chapter 32 of Gallian's book and the statement and proof of the Primitive Element Theorem (Theorem 21.6 on page 375 of Gallian's book) three times:
- First time as if you were reading a novel - quickly and without too much attention to detail, just to learn what the main keywords and concepts and goals are.
- Second time like you were studying for an exam on the subject - slowly and not skipping anything, verifying every little detail.
- And then a third time, again at a quicker pace, to remind yourself of the bigger picture all those little details are there to paint.
Doing
Solve problems 1, 4, 6#, 8#, 14#, 15#, 16 and 18 in Chapter 32 of Gallian's book but submit only the solutions of the problems marked with a sharp (#).
Due Date
This assignment is due in class on Wednesday April 11, 2007.
Just for Fun
1. Prove that the following two "pentagonal rubik's style" combinatorial games are always solvable:
2. Which of the following three "hexagonal rubik's style" combinatorial games are always solvable?