07-1352/Class Notes for February 27

07-1352/Navigation Panel   Back to 06-1350 # Week of... Links 1 Jan 9 About, Notes 2 Jan 16 Notes 3 Jan 23 Notes 4 Jan 30 Notes and Plans 5 Feb 6 Notes 6 Feb 13 Notes R Feb 20 Reading week 7 Feb 27 Notes 8 Mar 6 Notes 9 Mar 13 Notes 10 Mar 20 Notes 11 Mar 27 Notes 12 Apr 3 Map 13 Apr 10 Dancso SP Apr 17 Chu, Sankaran, Amir-Khosravi Suggested Student Topics

In Preparation

The information below is preliminary and cannot be trusted! (v)

Today's Agenda

• Today's material is separately simple and deep, therefore Dror will get the chance to butcher it twice.
• Recall the schematics of the Kontsevich Integral.
• Recall the fundamental theorem of finite type invariants for knotted trivalent graphs.
• The underlying basic truth, assuming a "naive" Kontsevich integral for framed trivalent graphs exists.
• A sophisticated construction of the "naive" object, using ideas from renormalization theory and the renormalization group.

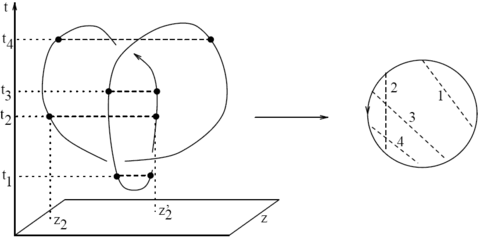
The Schematics of the Kontsevich Integral

$Z_{0}(K)=\ \ \ \ \ \ \ \ \ \ \int \!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\!\sum _{m;\ t_{1}<\ldots <t_{m};\ P=\{(z_{i},z'_{i})\}}{\frac {(-1)^{\#P_{\downarrow }}}{(2\pi i)^{m}}}D_{P}\bigwedge _{i=1}^{m}{\frac {dz_{i}-dz'_{i}}{z_{i}-z'_{i}}}$

The Fundamental Theorem of Finite Type Invariants for Knotted Trivalent Graphs

Almost Theorem. There exists a universal TG-morphism $Z=(Z_{\Gamma }):KTG\to {\mathcal {A}}$ from the TG-algebra of knotted trivalent graphs to the TG-algebra of Jacobi diagrams. Furthermore, any two such TG-morphisms are twist equivalent.

Theorem. (Essentially due to Murakami and Ohtsuki, [MO]; see also Dancso [Da]) There exists an R-normal TG-morphism $Z=(Z_{\Gamma }):KTG\to {\mathcal {A}}^{\nu }$ from the TG-algebra of knotted trivalent graphs to the $\nu$-twisted TG-algebra of Jacobi diagrams. Furthermore, any two such TG-morphisms are twist equivalent.

The above theorem is simply the accurate formulation of the almost theorem above it. The "almost theorem" is just what you would have expected, with an additional uniqueness statement. The "theorem" just adds to it a few normalizations that actually make it right. The determination of these normalizations is quite a feat; even defining them takes a page or two. I'm not entirely sure why the Gods of mathematics couldn't have just allowed the "almost theorem" to be true and make our lives a bit simpler.

Enough whining; we just need to define "R-normal" and ${\mathcal {A}}^{\nu }$.

Definition. $Z$ is called R-normal if Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle Z(\bigcirc)^{-1}Z(\MobiusSymbol)=\exp(\isolatedchord/4)} in ${\mathcal {A}}(\bigcirc )$, where Failed to parse (SVG (MathML can be enabled via browser plugin): Invalid response ("Math extension cannot connect to Restbase.") from server "https://wikimedia.org/api/rest_v1/":): {\displaystyle (\MobiusSymbol)} denotes the positively-twisted Möbius band and where Failed to parse (unknown function "\isolatedchord"): {\displaystyle (\isolatedchord)} denotes the unique degree 1 chord diagram in ${\mathcal {A}}(\bigcirc )$.

Definition. ${\mathcal {A}}^{\nu }$ is almost the same as ${\mathcal {A}}$. It has the same spaces (i.e., for any $\Gamma$, ${\mathcal {A}}^{\nu }(\Gamma )={\mathcal {A}}(\Gamma )$), but the unzip operations on ${\mathcal {A}}^{\nu }$ get "renormalized":

The edge-unzip operations.

Let $\nu$ denote the specific element of ${\mathcal {A}}(\uparrow )$ defined in the following subsection. If $u_{e}$ denotes the unzip operation of an edge $e$ for the TG-algebra ${\mathcal {A}}$ and $u_{e}^{\nu }$ is the corresponding operation in ${\mathcal {A}}^{\nu }$, the two operations are related by $u_{e}^{\nu }=\nu _{e'}^{-1/2}\nu _{e''}^{-1/2}u_{e}\nu _{e}^{1/2}$. Here "$\nu _{e}^{1/2}$" means "inject a copy of $\nu ^{1/2}$ on the edge $e$ of $\Gamma$, and likewise, "$\nu _{e'}^{-1/2}\nu _{e''}^{-1/2}$" means "inject copies of $\nu ^{-1/2}$ on the edges $e'$ and $e''$ of $u_{e}\Gamma$ that are created by the unzip of $e$".

References

[MO] ^  J. Murakami and T. Ohtsuki, Topological Quantum Field Theory for the Universal Quantum Invariant, Communications in Mathematical Physics 188 (1997) 501-520.