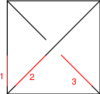
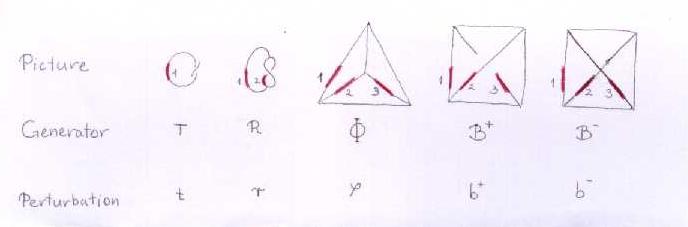
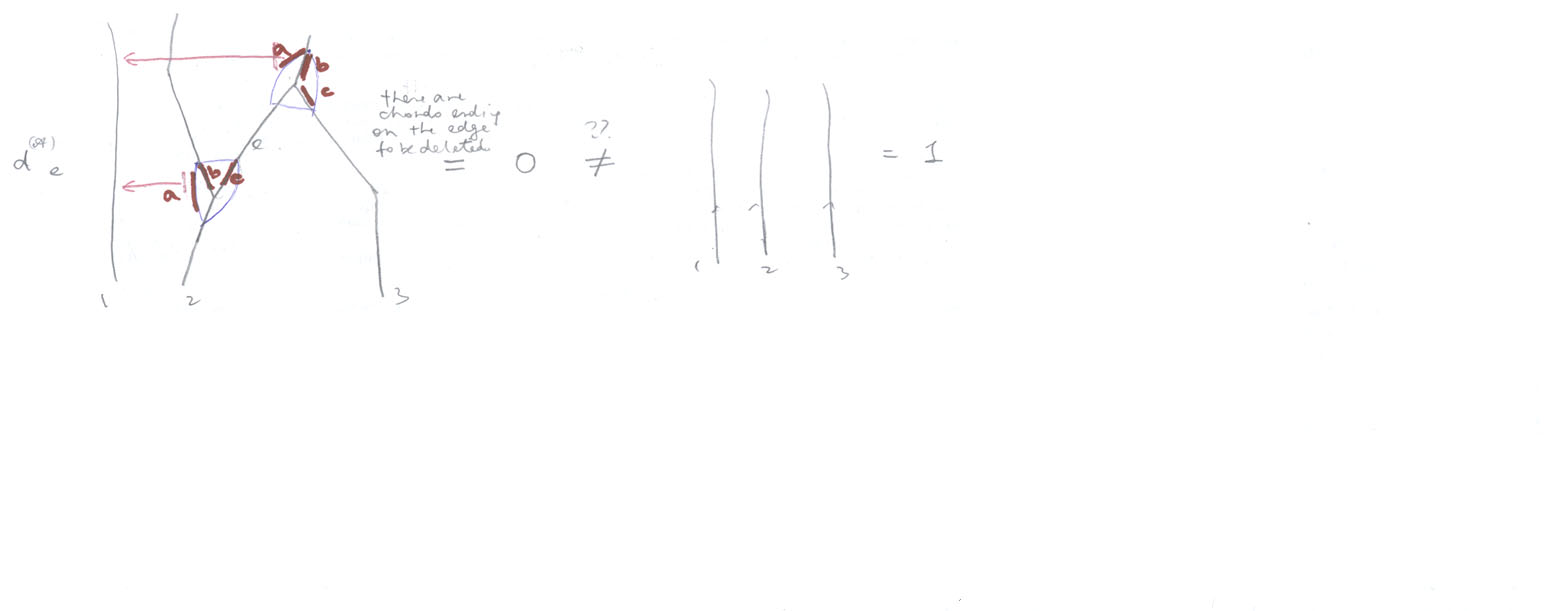The Generators
Our generators are  ,
,  ,
,  and
and  :
:
| Picture
|
|
|
|
|
|
| Generator
|

|

|

|

|

|
| Perturbation
|

|

|

|

|

|
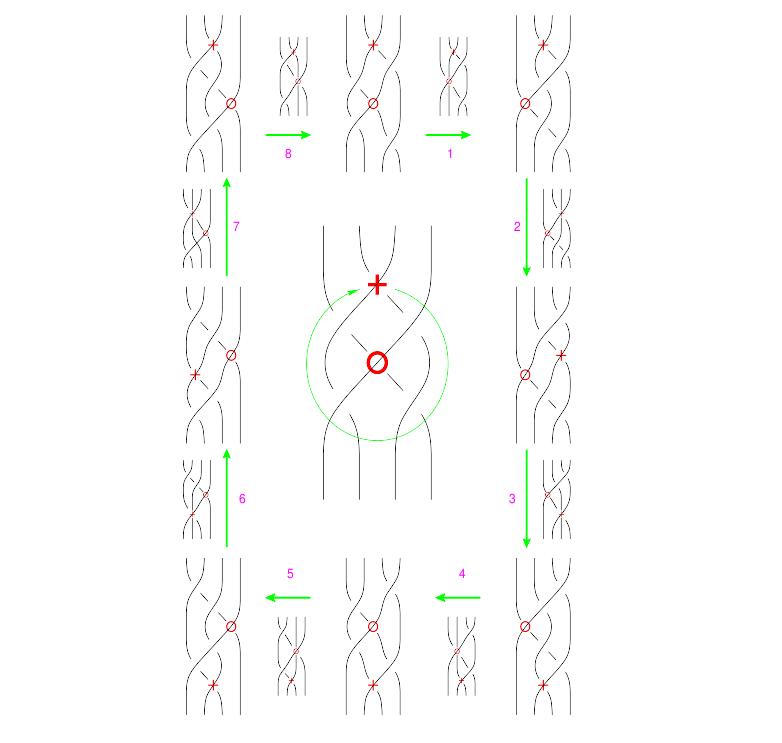
A low-tech completed version of this chart (Suzie's):
The Relations
The Symmetry of B (Suzie's)
To eliminate the choice involved in placing a B at a crossing, it has to have 180 degrees rotational symmetry. This yields the following picture:
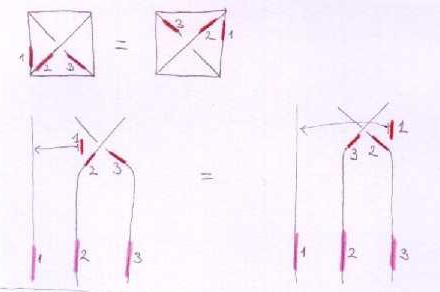
The relation cannot be written in the first notation, as on the right side the chords ending on different red lines could end up on the same pink line.
In the linearized functional notation though we can express this:

Explanation: on the right side, chords on the first red line can drop off on either the third, second or the first strand, morover, the orders are reversed, hence the minus signs.
The same picture for B^- yields:

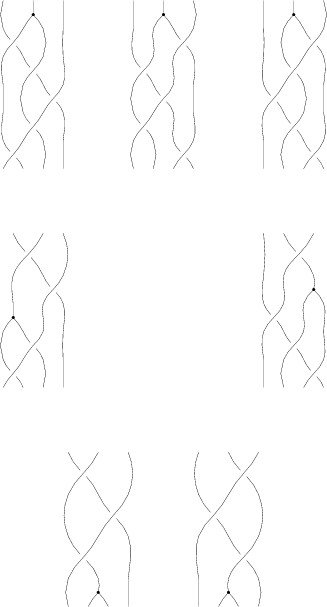
The symmetry of  (Suzie's)
(Suzie's)
 has to have A(4)-symmetry. For example, rotation around the "top" vertex yields the following picture and relation:
has to have A(4)-symmetry. For example, rotation around the "top" vertex yields the following picture and relation:
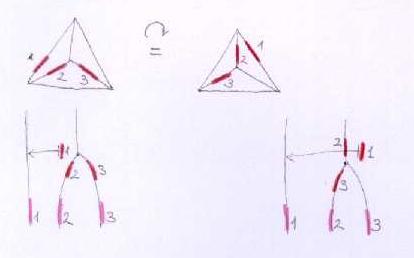
The same explanation goes here, and we get the relation:

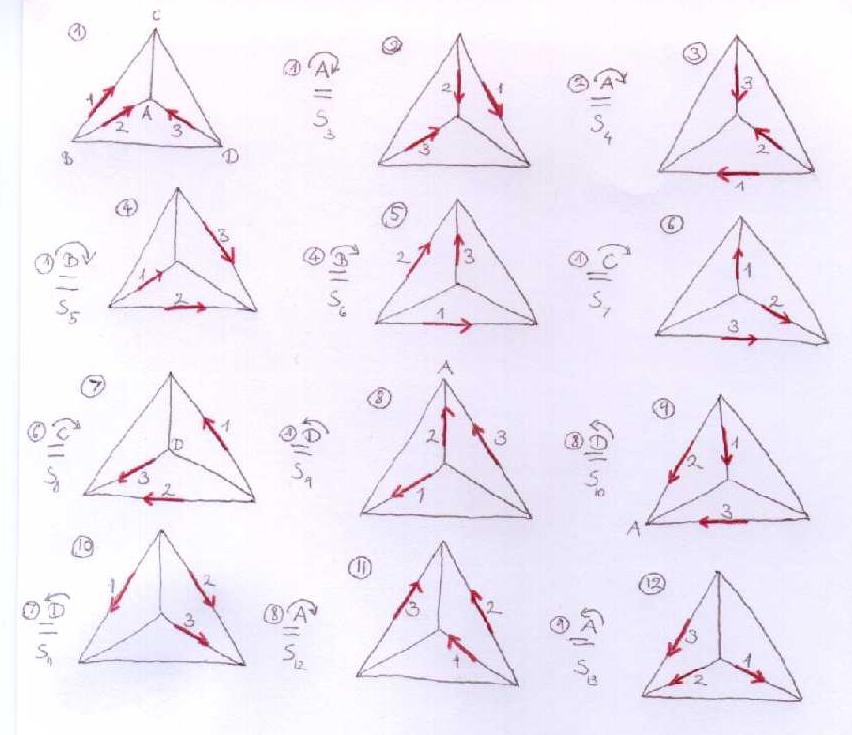
And here is the full picture and the relations (I suppose it would be enough to take a few that generate A(4), but we're on the safe side writing all these up... and I kind of got into drawing tetrahedrons.):











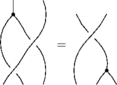
The Reidemeister move R1 (Suzie's)
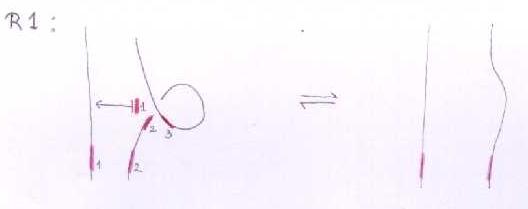
As with the symmetry relations, we cannot write this one in the first notation either.
In the linearized functional notation, it looks like this:

Where the negative sign is because the order of the chords is reversed as we slide them along the little loop.
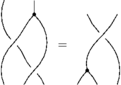
The Reidemeister move R2 (Suzie's)
With three sides of the shielding removed, the picture is:
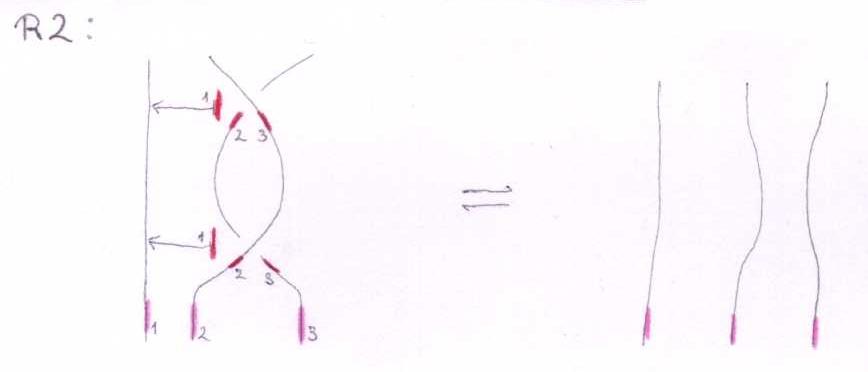
This means:

Linearized and in functional form:

And we get the other R2 by switching both crossings, i.e. switching b^+ and b^-:

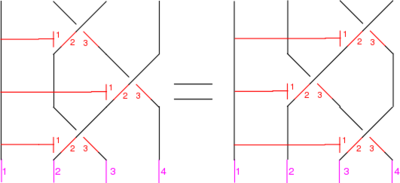
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|

|
|
|

|
The Reidemeister Move R4, source:Andy
First version of R4:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
Second version:
In formulas, this is
 .
.
Linearized and written in functional form, this becomes

|
The Operation unzip
Warning: I am not sure if this is correct, but thought it better to post than not post.
We have found the  ,
,  ,
, operations in the space
operations in the space  corresponding to the
corresponding to the  ,
, ,
,  , in the space of
, in the space of  , so that for the instance
, so that for the instance  :
:
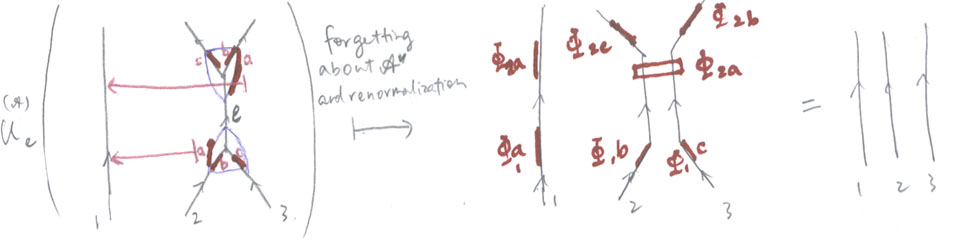
(on the LHS,I chose escapes routes for the chords ending on any shield first, then unzip in the space A (here I am not sure if I handled it correctly), and this should equal to the LHS: Z of the unzipped knot projection.)
Linearized and in functional form:

The part I don't quite understand:
When we unzip an edge with chords ending on it, we need to sum up all combinations of individual chords ending on the 2 unzipped edges; but here we have been treating the chords ending on an edge as just one single collection, so I only summed up the 2 ways of the collection ending on the unzipped edges
The Operation delete
Warning: sorry, I must be doing something wrong to obtain 0 on the LHS--since there are chords ending on the edge to be deleted, but non-zero on the RHS.
As above,  :
:
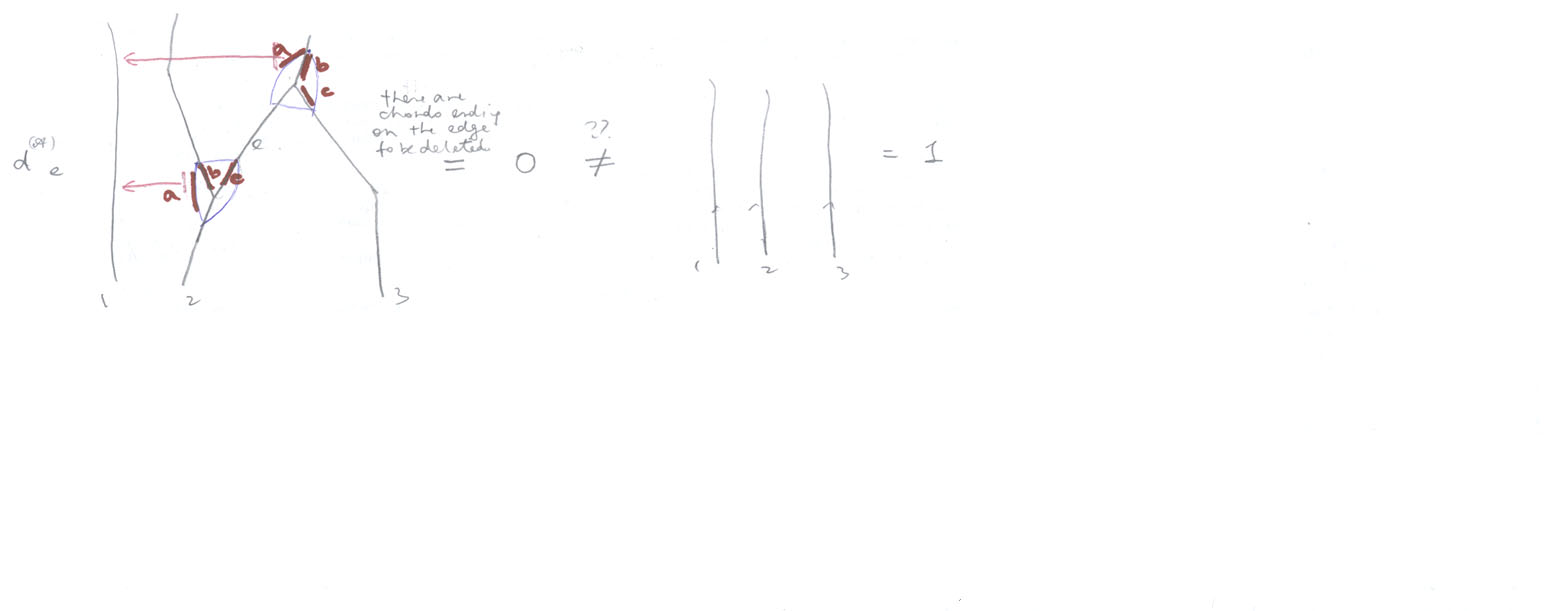
The Syzygies
The "B around B" Syzygy
The picture, with all shielding removed, is
|
|
(Drawn with Inkscape)
(note that lower quality pictures are also acceptable)
|
The functional form of this syzygy is

|

|
|
|

|
|
|

|
The " around B" Syzygy- I copy-pasted this from Andy, as well as R4
around B" Syzygy- I copy-pasted this from Andy, as well as R4
The picture, with all shielding (and any other helpful notations) removed, is
The functional form of this syzygy is

|

|
|
|

|
|
|

|
The " around
around  " Syzygy -also taken from Andy
" Syzygy -also taken from Andy
note: I've changed Andy's notation to fit my version of R2.
The picture is
The functional form of this syzygy is

|

|
|
|

|
|
|

|
|
|

|
|
|

|
Note that the first and last terms cancel, as the two steps at the top of the diagram are opposites.
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy,  . Copy paste it into a live Mathematica session to see that it's right!
. Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|