User:Andy/06-1350-HW4: Difference between revisions
(Added weird R2.) |
mNo edit summary |
||
| (2 intermediate revisions by the same user not shown) | |||
| Line 29: | Line 29: | ||
====The Reidemeister Move R2==== |
====The Reidemeister Move R2==== |
||
The following version of R2 was the easiest to use to |
The following version of R2 was the easiest to use to build my [[media:06-1350-PhiAroundPhi.png|original <math>\Phi</math> around <math>\Phi</math> syzygy]]: |
||
[[Image:06-1350-R2-weird.png|center]] |
[[Image:06-1350-R2-weird.png|center]] |
||
In formulas, this is |
In formulas, this is |
||
| Line 129: | Line 129: | ||
====The "<math>\Phi</math> around <math>\Phi</math>" Syzygy==== |
====The "<math>\Phi</math> around <math>\Phi</math>" Syzygy==== |
||
The original syzygy is available at [[:Image:06-1350-PhiAroundPhi.png]]. |
|||
The picture is |
|||
A cleaner, minimal picture is |
|||
{| align=center |
{| align=center |
||
|- align=center |
|- align=center |
||
|[[Image:06-1350- |
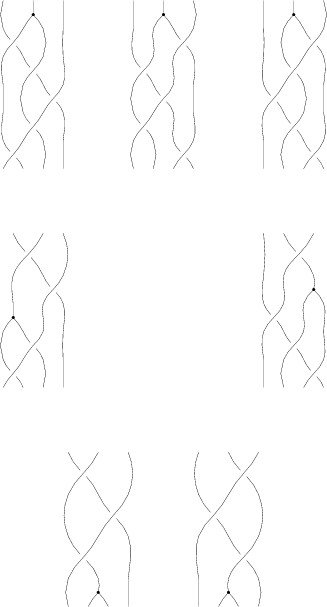
|[[Image:06-1350-PhiAroundPhiClean.png|center]] |
||
|- |
|- |
||
|align=right|(Drawn with [http://asymptote.sf.net/ Asymptote], [[06-1350/Syzygies in Asymptote|Syzygies in Asymptote]]) |
|align=right|(Drawn with [http://asymptote.sf.net/ Asymptote], [[06-1350/Syzygies in Asymptote|Syzygies in Asymptote]]) |
||
| Line 139: | Line 140: | ||
The functional form of this syzygy is |
The functional form of this syzygy is |
||
{| |
{|align=center |
||
|- |
|- |
||
|<math>\Phi\Phi(x_1,x_2,x_3,x_4,x_5) = </math> |
|<math>\Phi\Phi(x_1,x_2,x_3,x_4,x_5) = </math> |
||
|<math>\ |
|<math>\rho_{4b}(x_1+x_4,x_2,x_3,x_5) + \rho_{4b}(x_1,x_2,x_3,x_4) + \rho_{4a}(x_1,x_2+x_3,x_4,x_5)</math> |
||
|- |
|- |
||
| |
| |
||
|<math> |
|<math>- \rho_{4b}(x_1,x_2,x_3,x_4+x_5) - \rho_{4a}(x_1+x_2,x_3,x_4,x_5) - \rho_{4a}(x_1,x_2,x_4,x_5).</math> |
||
|- |
|||
| |
|||
|<math>+ \rho_{4a}(x_1,x_4+x_5,x_2,x_3) - \rho_{4b}(x_1,x_4,x_5,x_2+x_3) - \rho_{4a}(x_1+x_4,x_5,x_2,x_3)</math> |
|||
|- |
|||
| |
|||
|<math>- \rho_2(x_1+x_4,x_2,x_5) - \rho_2(x_1+x_2+x_4,x_3,x_5) - \rho_{4a}(x_1,x_4,x_2,x_3)</math> |
|||
|- |
|||
| |
|||
|<math>- \rho_2(x_1,x_2,x_4) - \rho_2(x_1+x_2,x_3,x_4)</math> |
|||
|} |
|} |
||
Note that the first and last terms cancel, as the top steps at the top of the diagram are opposites. |
|||
===A Mathematica Verification=== |
===A Mathematica Verification=== |
||
Latest revision as of 17:35, 5 December 2006
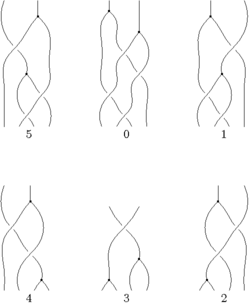
The Generators
Our generators are , , and :
| Picture | 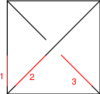
|
||||
| Generator | |||||
| Perturbation |
The Relations
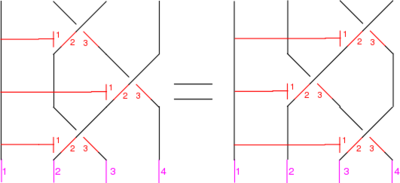
The Reidemeister Move R2
The following version of R2 was the easiest to use to build my original around syzygy:
In formulas, this is
Linearized and written in functional form, this becomes
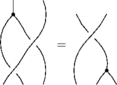
The Reidemeister Move R3
The picture (with three sides of the shielding removed) is
In formulas, this is
Linearized and written in functional form, this becomes
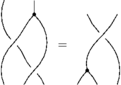
The Reidemeister Move R4
To establish the syzygy below, I needed two versions of R4. First:
In formulas, this is
Linearized and written in functional form, this becomes
Second:
In formulas, this is
Linearized and written in functional form, this becomes
Are these independent, or can they be shown to be equivalent using other relations?
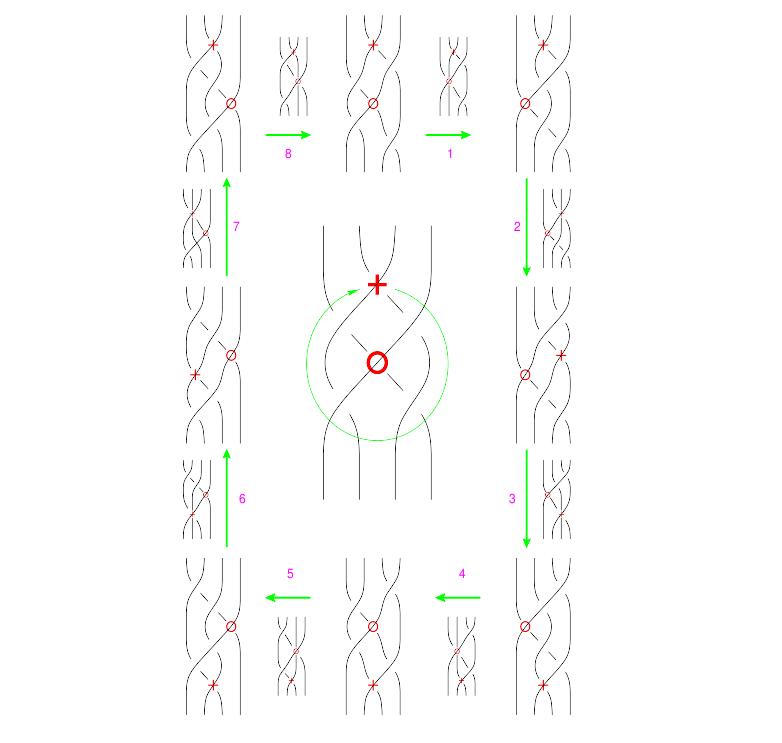
The Syzygies
The "B around B" Syzygy
The picture, with all shielding removed, is
| (Drawn with Inkscape) (note that lower quality pictures are also acceptable) |
The functional form of this syzygy is
The " around B" Syzygy
The picture, with all shielding (and any other helpful notations) removed, is
| (Drawn with Asymptote, Syzygies in Asymptote) |
The functional form of this syzygy is
The " around " Syzygy
The original syzygy is available at Image:06-1350-PhiAroundPhi.png. A cleaner, minimal picture is
| (Drawn with Asymptote, Syzygies in Asymptote) |
The functional form of this syzygy is
A Mathematica Verification
The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!
In[1]:=
|
d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};
|
In[3]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2
|
Out[3]=
|
- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]
|
In[4]:=
|
BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
|
Out[4]=
|
0
|