User:Andy/06-1350-HW4: Difference between revisions

From Drorbn
Jump to navigationJump to search
(Copied the assignment.)
 
mNo edit summary
 
(8 intermediate revisions by 2 users not shown)
Line 27: Line 27:


===The Relations===
===The Relations===

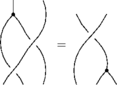
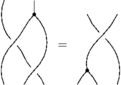
====The Reidemeister Move R2====
The following version of R2 was the easiest to use to build my [[media:06-1350-PhiAroundPhi.png|original <math>\Phi</math> around <math>\Phi</math> syzygy]]:
[[Image:06-1350-R2-weird.png|center]]
In formulas, this is
<center><math>1 = (123)^\star B^- (132)^\star B^+.</math></center>
Linearized and written in functional form, this becomes
{| align=center
|-
|<math>\rho_2(x_1,x_2,x_3) = - b^-(x_1,x_2,x_3) - b^+(x_1,x_3,x_2).</math>
|}


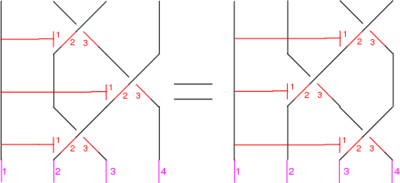
====The Reidemeister Move R3====
====The Reidemeister Move R3====
Line 42: Line 53:
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math>
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math>
|}
|}

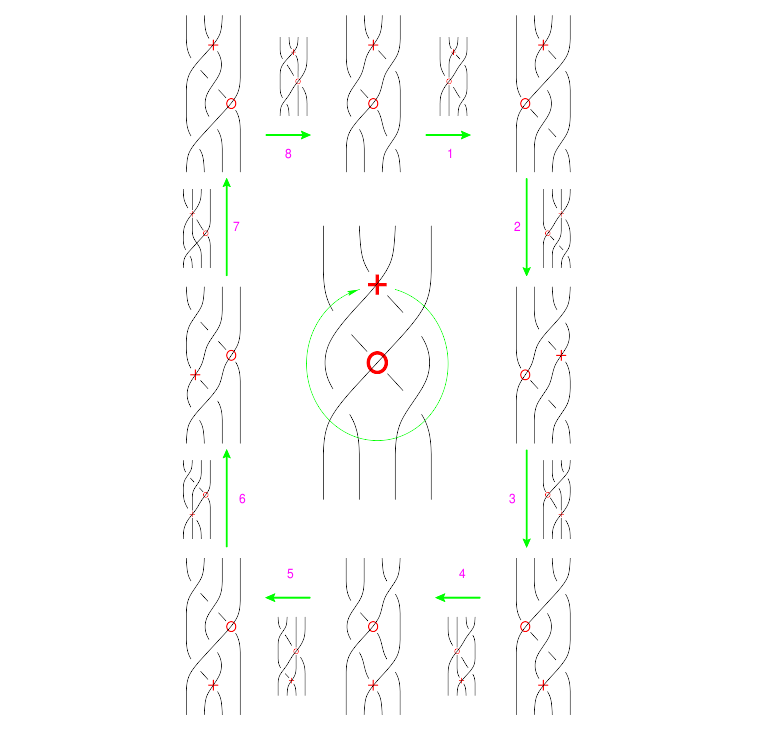
====The Reidemeister Move R4====
To establish the syzygy below, I needed two versions of R4. First:
[[Image:06-1350-R4a.png|center]]
In formulas, this is
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star \Phi = (1123)^\star \Phi (1233)^\star B^+</math>.</center>
Linearized and written in functional form, this becomes
{| align=center
|-
|<math>\rho_{4a}(x_1,x_2,x_3,x_4) = b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + \phi(x_1,x_3,x_4) - \phi(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_3+x_4).</math>
|}

Second:
[[Image:06-1350-R4b.png|center]]
In formulas, this is
<center><math>(1123)^\star B^+ (1203)^\star B^+ (1231)^\star \Phi = (1230)^\star \Phi (1223)^\star B^+</math>.</center>
Linearized and written in functional form, this becomes
{| align=center
|-
|<math>\rho_{4b}(x_1,x_2,x_3,x_4) = b^+(x_1+x_2,x_3,x_4) + b^+(x_1,x_2,x_4) + \phi(x_1+x_4,x_2,x_3) - \phi(x_1,x_2,x_3) - b^+(x_1,x_2+x_3,x_4).</math>
|}

Are these independent, or can they be shown to be equivalent using other relations?


===The Syzygies===
===The Syzygies===
Line 67: Line 101:
|
|
|<math>+ \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5).</math>
|<math>+ \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5).</math>
|}

====The "<math>\Phi</math> around B" Syzygy====

The picture, with all shielding (and any other helpful notations) removed, is
{| align=center
|- align=center
|[[Image:06-1350-PhiAroundB.png|center]]
|-
|align=right|(Drawn with [http://asymptote.sf.net/ Asymptote], [[06-1350/Syzygies in Asymptote|Syzygies in Asymptote]])
|}

The functional form of this syzygy is

{| align=center
|-
|<math>\Phi B(x_1,x_2,x_3,x_4,x_5) = </math>
|<math>\rho_3(x_1,x_2,x_3,x_5) + \rho_{4a}(x_1+x_5,x_2,x_3,x_4) + \rho_{4b}(x_1+x_2,x_3,x_4,x_5)</math>
|-
|
|<math>- \rho_3(x_1,x_2,x_3+x_4,x_5) - \rho_{4a}(x_1,x_2,x_3,x_4)</math>
|-
|
|<math>- \rho_{4b}(x_1,x_3,x_4,x_5) + \rho_3(x_1+x_3,x_2,x_4,x_5).</math>
|}

====The "<math>\Phi</math> around <math>\Phi</math>" Syzygy====

The original syzygy is available at [[:Image:06-1350-PhiAroundPhi.png]].
A cleaner, minimal picture is
{| align=center
|- align=center
|[[Image:06-1350-PhiAroundPhiClean.png|center]]
|-
|align=right|(Drawn with [http://asymptote.sf.net/ Asymptote], [[06-1350/Syzygies in Asymptote|Syzygies in Asymptote]])
|}

The functional form of this syzygy is

{|align=center
|-
|<math>\Phi\Phi(x_1,x_2,x_3,x_4,x_5) = </math>
|<math>\rho_{4b}(x_1+x_4,x_2,x_3,x_5) + \rho_{4b}(x_1,x_2,x_3,x_4) + \rho_{4a}(x_1,x_2+x_3,x_4,x_5)</math>
|-
|
|<math>- \rho_{4b}(x_1,x_2,x_3,x_4+x_5) - \rho_{4a}(x_1+x_2,x_3,x_4,x_5) - \rho_{4a}(x_1,x_2,x_4,x_5).</math>
|}
|}


Latest revision as of 17:35, 5 December 2006

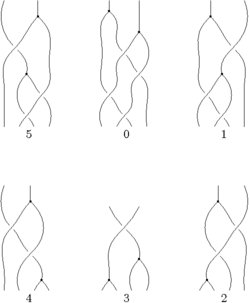
The Generators

Our generators are , , and :

Picture 06-1350-BPlus.svg
Generator
Perturbation

The Relations

The Reidemeister Move R2

The following version of R2 was the easiest to use to build my original around syzygy:

06-1350-R2-weird.png

In formulas, this is

Linearized and written in functional form, this becomes

The Reidemeister Move R3

The picture (with three sides of the shielding removed) is

06-1350-R4.svg

In formulas, this is

.

Linearized and written in functional form, this becomes

The Reidemeister Move R4

To establish the syzygy below, I needed two versions of R4. First:

06-1350-R4a.png

In formulas, this is

.

Linearized and written in functional form, this becomes

Second:

06-1350-R4b.png

In formulas, this is

.

Linearized and written in functional form, this becomes

Are these independent, or can they be shown to be equivalent using other relations?

The Syzygies

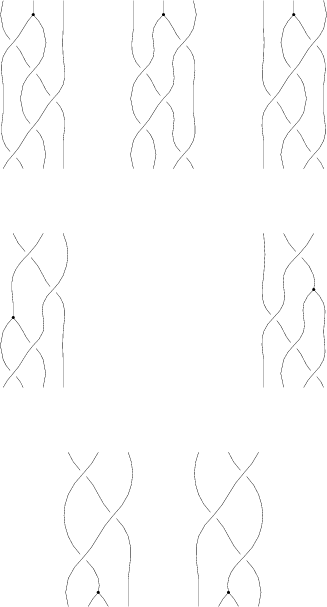
The "B around B" Syzygy

The picture, with all shielding removed, is

06-1350-BAroundB.svg
(Drawn with Inkscape)
(note that lower quality pictures are also acceptable)

The functional form of this syzygy is

The " around B" Syzygy

The picture, with all shielding (and any other helpful notations) removed, is

06-1350-PhiAroundB.png
(Drawn with Asymptote, Syzygies in Asymptote)

The functional form of this syzygy is

The " around " Syzygy

The original syzygy is available at Image:06-1350-PhiAroundPhi.png. A cleaner, minimal picture is

06-1350-PhiAroundPhiClean.png
(Drawn with Asymptote, Syzygies in Asymptote)

The functional form of this syzygy is

A Mathematica Verification

The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!

In[1]:= d1 = { rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] }; d2 = { BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] };
In[3]:= BAroundB[x1, x2, x3, x4, x5] /. d2
Out[3]= - rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] + rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4]
In[4]:= BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
Out[4]= 0
Retrieved from "https://drorbn.net/index.php?title=User:Andy/06-1350-HW4&oldid=3067"