User:Drorbn/06-1350-HW4: Difference between revisions

From Drorbn
Jump to navigationJump to search
No edit summary
 
(12 intermediate revisions by the same user not shown)
Line 1: Line 1:
===The Generators===
===The Generators===


Our generators are <math>T</math>, <math>R</math>, <math>Y=\Phi</math> and <math>B^{\pm}</math>. (You might consider splitting <math>Y</math> into two, <math>Y^{up}</math> and <math>Y^{dn}</math>). In pictures, they are
Our generators are <math>T</math>, <math>R</math>, <math>\Phi</math> and <math>B^{\pm}</math>:
{| align=center
{| align=center cellpadding=10 style="border: solid orange 1px"
|- align=center
|- align=center valign=middle
|align=left|Picture
⚫
|
|
|
|
|
Line 10: Line 10:
|[[Image:06-1350-BPlus.svg|100px]]
|[[Image:06-1350-BPlus.svg|100px]]
|
|
|- align=center
|- align=center valign=middle
|align=left|Generator
|<math>T</math>
|<math>T</math>
|<math>R</math>
|<math>R</math>
|<math>Y^{up}</math>
|<math>\Phi</math>
⚫
|<math>Y^{dn}</math>
|<math>B^+</math>
|<math>B^+</math>
|<math>B^-</math>
|<math>B^-</math>
|- align=center valign=middle
|align=left|Perturbation
|<math>t</math>
|<math>r</math>
|<math>\varphi</math>
⚫
|<math>b^+</math>
|<math>b^-</math>
|}
|}


Line 22: Line 29:


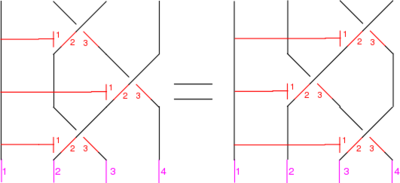
====The Reidemeister Move R3====
====The Reidemeister Move R3====
The picture is
The picture (with three sides of the shielding removed) is
[[Image:06-1350-R4.svg|400px|center]]
[[Image:06-1350-R4.svg|400px|center]]
In formulas, this is
In formulas, this is
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+</math>.</center>
<center><math>(1230)^\star B^+ (1213)^\star B^+ (1023)^\star B^+ = (1123)^\star B^+ (1203)^\star B^+ (1231)^\star B^+</math>.</center>
Linearized and written in functional form, this becomes
Thus the R3 component of <math>d</math> is
{| align=center
<center><math>(1230)^\star b^+ +(1213)^\star b^+ +(1023)^\star b^+ -(1123)^\star b^+ -(1203)^\star b^+ -(1231)^\star b^+</math>.</center>
|-
|<math>\rho_3(x_1, x_2, x_3, x_4) = </math>
|<math>b^+(x_1,x_2,x_3) + b^+(x_1+x_3,x_2,x_4) + b^+(x_1,x_3,x_4)</math>
|-
⚫
|
|<math>- b^+(x_1+x_2,x_3,x_4) - b^+(x_1,x_2,x_4) - b^+(x_1+x_4,x_2,x_3).</math>
|}


===The Syzygies===
===The Syzygies===

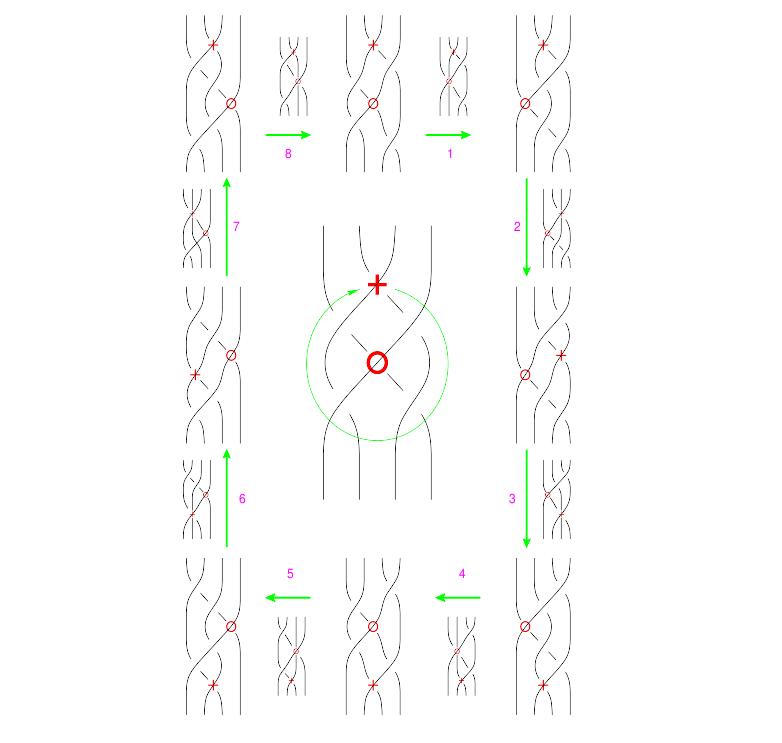
====The "B around B" Syzygy====

The picture, with all shielding removed, is
{| align=center
|- align=center
|[[Image:06-1350-BAroundB.svg|center]]
|-
|align=right|(Drawn with [http://www.inkscape.org/ Inkscape])<br>(note that lower quality pictures are also acceptable)
|}

The functional form of this syzygy is

{| align=center
|-
|<math>BB(x_1,x_2,x_3,x_4,x_5) = </math>
|<math>\rho_3(x_1, x_2, x_3, x_5) + \rho_3(x_1 + x_5, x_2, x_3, x_4) - \rho_3(x_1 + x_2, x_3, x_4, x_5)</math>
|-
|
|<math>- \rho_3(x_1, x_2, x_4, x_5) - \rho_3(x_1 + x_4, x_2, x_3, x_5) - \rho_3(x_1, x_2, x_3, x_4)</math>
|-
|
|<math>+ \rho_3(x_1, x_3, x_4, x_5) + \rho_3(x_1 + x_3, x_2, x_4, x_5).</math>
|}


===A Mathematica Verification===
===A Mathematica Verification===

The following simulated Mathematica session proves that for our single relation and single syzygy, <math>d^2=0</math>. Copy paste it into a live Mathematica session to see that it's right!

{{In|n=1|in=<nowiki>d1 = {
rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] +
bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] -
bp[x1 + x4, x2, x3]
};
d2 = {
BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] +
rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] -
rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] -
rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] +
rho3[x1 + x3, x2, x4, x5]
};</nowiki>}}

{{InOut|n=3|in=<nowiki>BAroundB[x1, x2, x3, x4, x5] /. d2</nowiki>|out=<nowiki>- rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5]
+ rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5]
+ rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5]
+ rho3[x1 + x5, x2, x3, x4]</nowiki>}}

{{InOut|n=4|in=<nowiki>BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1</nowiki>|out=<nowiki>0</nowiki>}}

Latest revision as of 18:41, 20 November 2006

The Generators

Our generators are , , and :

Picture 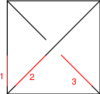06-1350-BPlus.svg
Generator
Perturbation

The Relations

The Reidemeister Move R3

The picture (with three sides of the shielding removed) is

06-1350-R4.svg

In formulas, this is

.

Linearized and written in functional form, this becomes

The Syzygies

The "B around B" Syzygy

The picture, with all shielding removed, is

06-1350-BAroundB.svg
(Drawn with Inkscape)
(note that lower quality pictures are also acceptable)

The functional form of this syzygy is

A Mathematica Verification

The following simulated Mathematica session proves that for our single relation and single syzygy, . Copy paste it into a live Mathematica session to see that it's right!

In[1]:= d1 = { rho3[x1_, x2_, x3_, x4_] :> bp[x1, x2, x3] + bp[x1 + x3, x2, x4] + bp[x1, x3, x4] - bp[x1 + x2, x3, x4] - bp[x1, x2, x4] - bp[x1 + x4, x2, x3] }; d2 = { BAroundB[x1_, x2_, x3_, x4_, x5_] :> rho3[x1, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4] - rho3[x1 + x2, x3, x4, x5] - rho3[x1, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] - rho3[x1, x2, x3, x4] + rho3[x1, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] };
In[3]:= BAroundB[x1, x2, x3, x4, x5] /. d2
Out[3]= - rho3[x1, x2, x3, x4] + rho3[x1, x2, x3, x5] - rho3[x1, x2, x4, x5] + rho3[x1, x3, x4, x5] - rho3[x1 + x2, x3, x4, x5] + rho3[x1 + x3, x2, x4, x5] - rho3[x1 + x4, x2, x3, x5] + rho3[x1 + x5, x2, x3, x4]
In[4]:= BAroundB[x1, x2, x3, x4, x5] /. d2 /. d1
Out[4]= 0
Retrieved from "https://drorbn.net/index.php?title=User:Drorbn/06-1350-HW4&oldid=2836"