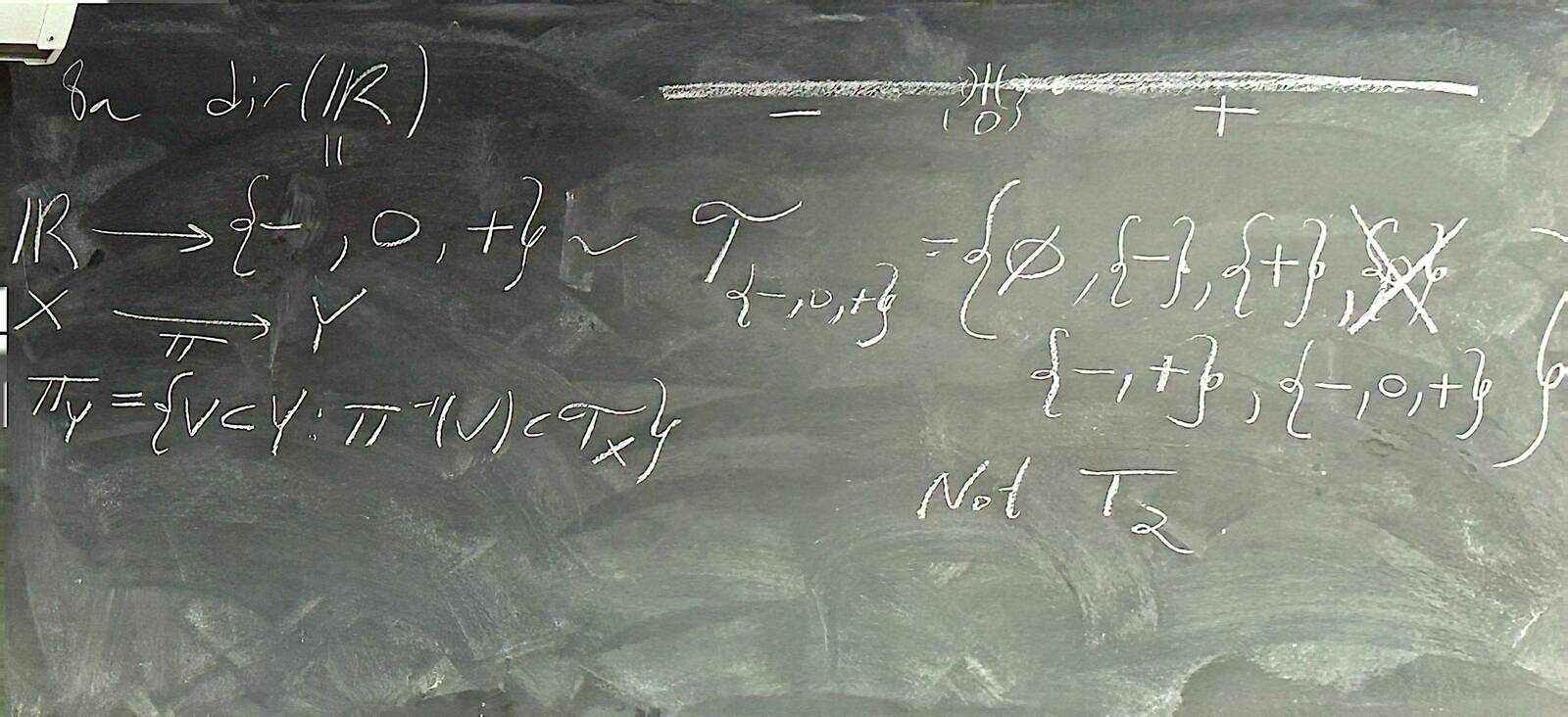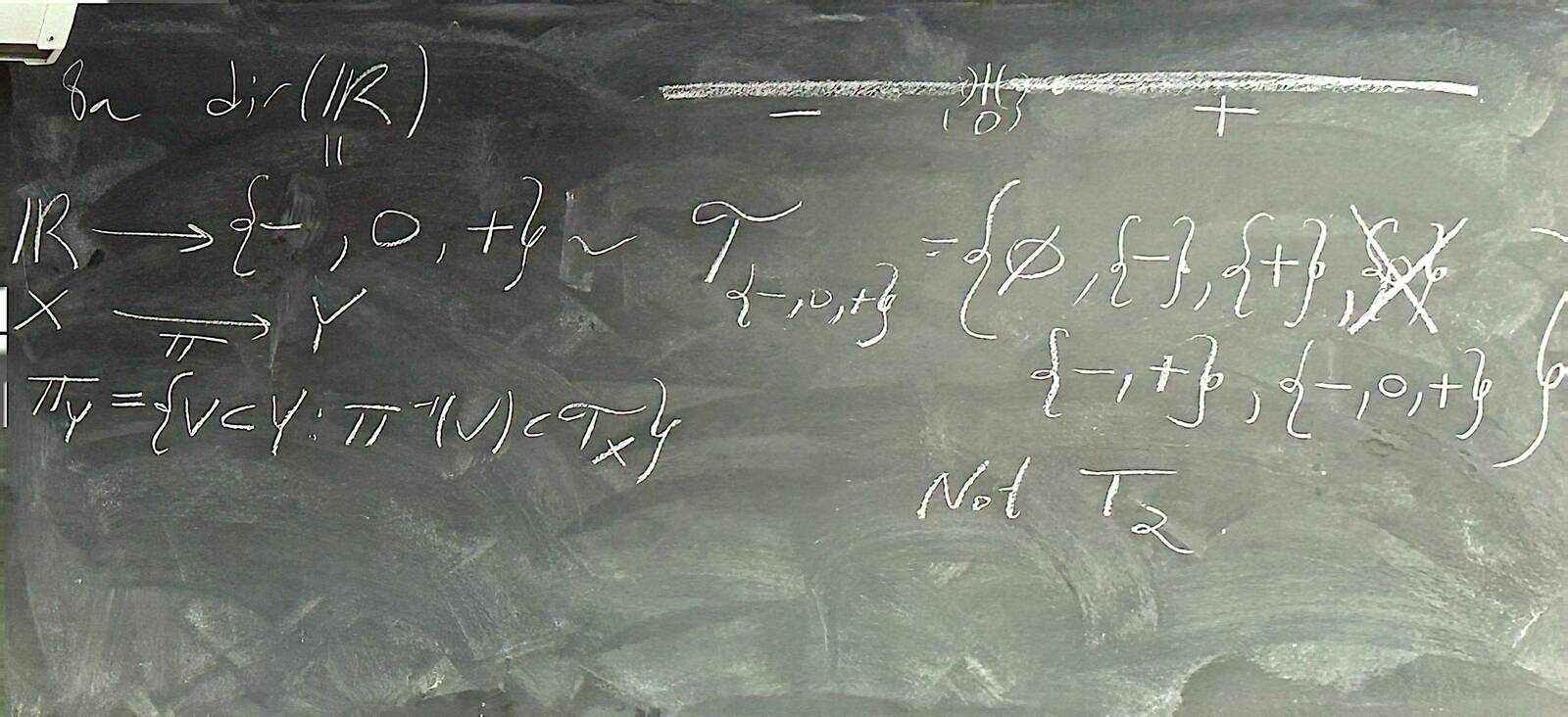
| 24-327-{ | hide text |
| 241201-152703: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (12). |
| 241201-152655: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (11). |
| 241201-152647: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (10). |
| 241201-152636: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (9). |
| 241201-152630: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (8). |
| 241201-152624: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (7). |
| 241201-152617: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (6). |
| 241201-152611: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (5). |
| 241201-152603: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (4). |
| 241201-152557: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (3). |
| 241201-152550: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim (2). |
| 241201-152535: | Thu Nov 28 H35-36: Retracts, Brouwer, and Lim. |
| 241128-063422: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (10). |
| 241128-063421: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (9). |
| 241128-063420: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (8). |
| 241128-063419: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (7). |
| 241128-063418: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (6). |
| 241128-063417: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (5). |
| 241128-063416: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (4). |
| 241128-063415: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (3). |
| 241128-063414: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts (2). |
| 241128-063413: | Tue Nov 26 H34: $\pi_1$ is a functor, retracts. |
| 241121-175656: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (18). |
| 241121-175655: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (17). |
| 241121-175654: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (16). |
| 241121-175653: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (15). |
| 241121-175652: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (14). |
| 241121-175651: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (13). |
| 241121-175650: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (12). |
| 241121-175649: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (11). |
| 241121-175648: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (10). |
| 241121-175647: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (9). |
| 241121-175646: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (8). |
| 241121-175645: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (7). |
| 241121-175644: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (6). |
| 241121-175643: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (5). |
| 241121-175642: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (4). |
| 241121-175641: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (3). |
| 241121-175640: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories (2). |
| 241121-175639: | Thu Nov 21 H32-33: $\pi_1(S^1)$, categories. |
| 241120-062923: | Tue Nov 19 H31: Lifting properties (9). |
| 241120-062922: | Tue Nov 19 H31: Lifting properties (8). |
| 241120-062921: | Tue Nov 19 H31: Lifting properties (7). |
| 241120-062920: | Tue Nov 19 H31: Lifting properties (6). |
| 241120-062919: | Tue Nov 19 H31: Lifting properties (5). |
| 241120-062918: | Tue Nov 19 H31: Lifting properties (4). |
| 241120-062917: | Tue Nov 19 H31: Lifting properties (3). |
| 241120-062916: | Tue Nov 19 H31: Lifting properties (2). |
| 241120-062915: | Tue Nov 19 H31: Lifting properties. |
| 241114-162740: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (15). |
| 241114-162739: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (14). |
| 241114-162738: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (13). |
| 241114-162737: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (12). |
| 241114-162736: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (11). |
| 241114-162735: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (10). |
| 241114-162734: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (9). |
| 241114-162733: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (8). |
| 241114-162732: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (7). |
| 241114-162731: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (6). |
| 241114-162730: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (5). |
| 241114-162729: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (4). |
| 241114-162728: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (3). |
| 241114-162727: | Thu Nov 14 H19-30: $\pi_1$, covering spaces (2). |
| 241114-162726: | Thu Nov 14 H19-30: $\pi_1$, covering spaces. |
| 241112-165040: | Tue Nov 12 H28: More on path homotopies (9). |
| 241112-165039: | Tue Nov 12 H28: More on path homotopies (8). |
| 241112-165038: | Tue Nov 12 H28: More on path homotopies (7). |
| 241112-165037: | Tue Nov 12 H28: More on path homotopies (6). |
| 241112-165036: | Tue Nov 12 H28: More on path homotopies (5). |
| 241112-165035: | Tue Nov 12 H28: More on path homotopies (4). |
| 241112-165034: | Tue Nov 12 H28: More on path homotopies (3). |
| 241112-165033: | Tue Nov 12 H28: More on path homotopies (2). |
| 241112-165032: | Tue Nov 12 H28: More on path homotopies. |
| 241107-162414: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (17) |
| 241107-162413: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (16) |
| 241107-162412: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (15) |
| 241107-162411: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (14) |
| 241107-162410: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (13) |
| 241107-162409: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (12) |
| 241107-162408: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (11) |
| 241107-162407: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (10) |
| 241107-162406: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (9) |
| 241107-162405: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (8) |
| 241107-162404: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (7) |
| 241107-162403: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (6) |
| 241107-162402: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (5) |
| 241107-162401: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (4) |
| 241107-162400: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (3) |
| 241107-162359: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies (2) |
| 241107-162358: | Thu Nov 7 H26-27: A bit on groups and a bit on homotopies |
| 241105-161906: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (10). |
| 241105-161905: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (9). |
| 241105-161904: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (8). |
| 241105-161903: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (7). |
| 241105-161902: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (6). |
| 241105-161901: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (5). |
| 241105-161900: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (4). |
| 241105-161859: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (3). |
| 241105-161858: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets (2). |
| 241105-161857: | Tue Nov 5 H25: Uniform continuity and the Lebesgue number lemma, regrets. |
| 241024-171201: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (20). |
| 241024-171200: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (19). |
| 241024-171159: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (18). |
| 241024-171158: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (17). |
| 241024-171157: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (16). |
| 241024-171156: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (15). |
| 241024-171155: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (14). |
| 241024-171154: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (13). |
| 241024-171153: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (12). |
| 241024-171152: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (11). |
| 241024-171151: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (10). |
| 241024-171150: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (9). |
| 241024-171149: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (8). |
| 241024-171148: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (7). |
| 241024-171147: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (6). |
| 241024-171146: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (5). |
| 241024-171145: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (4). |
| 241024-171144: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (3). |
| 241024-171143: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$ (2). |
| 241024-171142: | Thu Oct 24 H23-24: Compactness in ${\mathbb R}^n$. |
| 241022-165825: | Oct 22 H22: Compactness basics (12). |
| 241022-165824: | Oct 22 H22: Compactness basics (11). |
| 241022-165823: | Oct 22 H22: Compactness basics (10). |
| 241022-165822: | Oct 22 H22: Compactness basics (9). |
| 241022-165821: | Oct 22 H22: Compactness basics (8). |
| 241022-165820: | Oct 22 H22: Compactness basics (7). |
| 241022-165819: | Oct 22 H22: Compactness basics (6). |
| 241022-165818: | Oct 22 H22: Compactness basics (5). |
| 241022-165817: | Oct 22 H22: Compactness basics (4). |
| 241022-165816: | Oct 22 H22: Compactness basics (3). |
| 241022-165815: | Oct 22 H22: Compactness basics (2). |
| 241022-165814: | Oct 22 H22: Compactness basics. |
| 241019-080032: | Connectedness and products (19). |
| 241019-080031: | Connectedness and products (18). |
| 241019-080030: | Connectedness and products (17). |
| 241019-080029: | Connectedness and products (16). |
| 241019-080028: | Connectedness and products (15). |
| 241019-080027: | Connectedness and products (14). |
| 241019-080026: | Connectedness and products (13). |
| 241019-080025: | Connectedness and products (12). |
| 241019-080024: | Connectedness and products (11). |
| 241019-080023: | Connectedness and products (10). |
| 241019-080022: | Connectedness and products (9). |
| 241019-080021: | Connectedness and products (8). |
| 241019-080020: | Connectedness and products (7). |
| 241019-080019: | Connectedness and products (6). |
| 241019-080018: | Connectedness and products (5). |
| 241019-080017: | Connectedness and products (4). |
| 241019-080016: | Connectedness and products (3). |
| 241019-080015: | Connectedness and products (2). |
| 241019-080014: | Connectedness and products. |
| 241015-212829: | Tue Oct 15 H19: Connected spaces (10). |
| 241015-212828: | Tue Oct 15 H19: Connected spaces (9). |
| 241015-212827: | Tue Oct 15 H19: Connected spaces (8). |
| 241015-212826: | Tue Oct 15 H19: Connected spaces (7). |
| 241015-212825: | Tue Oct 15 H19: Connected spaces (6). |
| 241015-212824: | Tue Oct 15 H19: Connected spaces (5). |
| 241015-212823: | Tue Oct 15 H19: Connected spaces (4). |
| 241015-212822: | Tue Oct 15 H19: Connected spaces (3). |
| 241015-212821: | Tue Oct 15 H19: Connected spaces (2). |
| 241015-212820: | Tue Oct 15 H19: Connected spaces. |
| 241010-173958: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (17). |
| 241010-173957: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (16). |
| 241010-173956: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (15). |
| 241010-173955: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (14). |
| 241010-173954: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (13). |
| 241010-173953: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (12). |
| 241010-173952: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (11). |
| 241010-173951: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (10). |
| 241010-173950: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (9). |
| 241010-173949: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (8). |
| 241010-173948: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (7). |
| 241010-173947: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (6). |
| 241010-173946: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (5). |
| 241010-173945: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (4). |
| 241010-173944: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (3). |
| 241010-173943: | Thu Oct 10 H17-18: Quotient spaces, connected spaces (2). |
| 241010-173942: | Thu Oct 10 H17-18: Quotient spaces, connected spaces. |
| 241009-062543: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (9). |
| 241009-062542: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (8). |
| 241009-062541: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (7). |
| 241009-062540: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (6). |
| 241009-062539: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (5). |
| 241009-062538: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (4). |
| 241009-062537: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (3). |
| 241009-062536: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces (2). |
| 241009-062535: | Tue Oct 8 H16: Metrizabilifty and products, quotient spaces. |
| 241003-185843: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (19). |
| 241003-185842: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (18). |
| 241003-185841: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (17). |
| 241003-185840: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (16). |
| 241003-185839: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (15). |
| 241003-185838: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (14). |
| 241003-185837: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (13). |
| 241003-185836: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (12). |
| 241003-185835: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (11). |
| 241003-185834: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (10). |
| 241003-185833: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (9). |
| 241003-185832: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (8). |
| 241003-185831: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (7). |
| 241003-185830: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (6). |
| 241003-185829: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (5). |
| 241003-185828: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (4). |
| 241003-185827: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (3). |
| 241003-185826: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products (2). |
| 241003-185825: | Thu Oct 3 H14-15: Metrizability, sequential closure, and products. |
| 241001-163841: | Tue Oct 1 H13: Products, metric spaces (6). |
| 241001-163840: | Tue Oct 1 H13: Products, metric spaces (5). |
| 241001-163839: | Tue Oct 1 H13: Products, metric spaces (4). |
| 241001-163838: | Tue Oct 1 H13: Products, metric spaces (3). |
| 241001-163837: | Tue Oct 1 H13: Products, metric spaces (2). |
| 241001-163836: | Tue Oct 1 H13: Products, metric spaces. |
| 240927-141129: | Continuity, products and the axiom of Choice, the box and the cylinder topology (18). |
| 240927-141128: | Continuity, products and the axiom of Choice, the box and the cylinder topology (17). |
| 240927-141127: | Continuity, products and the axiom of Choice, the box and the cylinder topology (16). |
| 240927-141126: | Continuity, products and the axiom of Choice, the box and the cylinder topology (15). |
| 240927-141125: | Continuity, products and the axiom of Choice, the box and the cylinder topology (14). |
| 240927-141124: | Continuity, products and the axiom of Choice, the box and the cylinder topology (13). |
| 240927-141123: | Continuity, products and the axiom of Choice, the box and the cylinder topology (12). |
| 240927-141122: | Continuity, products and the axiom of Choice, the box and the cylinder topology (11). |
| 240927-141121: | Continuity, products and the axiom of Choice, the box and the cylinder topology (10). |
| 240927-141120: | Continuity, products and the axiom of Choice, the box and the cylinder topology (9). |
| 240927-141119: | Continuity, products and the axiom of Choice, the box and the cylinder topology (8). |
| 240927-141118: | Continuity, products and the axiom of Choice, the box and the cylinder topology (7). |
| 240927-141117: | Continuity, products and the axiom of Choice, the box and the cylinder topology (6). |
| 240927-141116: | Continuity, products and the axiom of Choice, the box and the cylinder topology (5). |
| 240927-141115: | Continuity, products and the axiom of Choice, the box and the cylinder topology (4). |
| 240927-141114: | Continuity, products and the axiom of Choice, the box and the cylinder topology (3). |
| 240927-141113: | Continuity, products and the axiom of Choice, the box and the cylinder topology (2). |
| 240927-141112: | Continuity, products and the axiom of Choice, the box and the cylinder topology. |
| 240925-061656: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (10). |
| 240925-061655: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (9). |
| 240925-061654: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (8). |
| 240925-061653: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (7). |
| 240925-061652: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (6). |
| 240925-061651: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (5). |
| 240925-061650: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (4). |
| 240925-061649: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (3). |
| 240925-061648: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces (2). |
| 240925-061647: | Class of Tuesday Septembet 24: Limit points, Hausdorff spaces. |
| 240919-221641: | Class of Thursday September 19: Closed sets (17). |
| 240919-221639: | Class of Thursday September 19: Closed sets (16). |
| 240919-221638: | Class of Thursday September 19: Closed sets (15). |
| 240919-221637: | Class of Thursday September 19: Closed sets (14). |
| 240919-221636: | Class of Thursday September 19: Closed sets (13). |
| 240919-221635: | Class of Thursday September 19: Closed sets (12). |
| 240919-221634: | Class of Thursday September 19: Closed sets (11). |
| 240919-221633: | Class of Thursday September 19: Closed sets (10). |
| 240919-221632: | Class of Thursday September 19: Closed sets (9). |
| 240919-221631: | Class of Thursday September 19: Closed sets (8). |
| 240919-221630: | Class of Thursday September 19: Closed sets (7). |
| 240919-221629: | Class of Thursday September 19: Closed sets (6). |
| 240919-221628: | Class of Thursday September 19: Closed sets (5). |
| 240919-221627: | Class of Thursday September 19: Closed sets (4). |
| 240919-221626: | Class of Thursday September 19: Closed sets (3). |
| 240919-221625: | Class of Thursday September 19: Closed sets (2). |
| 240919-221624: | Class of Thursday September 19: Closed sets. |
| 240917-163034: | Class of Tuesday September 17: Mostly the subspace topology (8). |
| 240917-163033: | Class of Tuesday September 17: Mostly the subspace topology (7). |
| 240917-163032: | Class of Tuesday September 17: Mostly the subspace topology (6). |
| 240917-163031: | Class of Tuesday September 17: Mostly the subspace topology (5). |
| 240917-163030: | Class of Tuesday September 17: Mostly the subspace topology (4). |
| 240917-163029: | Class of Tuesday September 17: Mostly the subspace topology (3). |
| 240917-163028: | Class of Tuesday September 17: Mostly the subspace topology (2). |
| 240917-163027: | Class of Tuesday September 17: Mostly the subspace topology. |
| 240912-183855: | Class of Thursday September 12: Bases, Orders, Products (18). |
| 240912-183854: | Class of Thursday September 12: Bases, Orders, Products (17). |
| 240912-183853: | Class of Thursday September 12: Bases, Orders, Products (16). |
| 240912-183852: | Class of Thursday September 12: Bases, Orders, Products (15). |
| 240912-183851: | Class of Thursday September 12: Bases, Orders, Products (14). |
| 240912-183850: | Class of Thursday September 12: Bases, Orders, Products (13). |
| 240912-183849: | Class of Thursday September 12: Bases, Orders, Products (12). |
| 240912-183848: | Class of Thursday September 12: Bases, Orders, Products (11). |
| 240912-183847: | Class of Thursday September 12: Bases, Orders, Products (10). |
| 240912-183846: | Class of Thursday September 12: Bases, Orders, Products (9). |
| 240912-183845: | Class of Thursday September 12: Bases, Orders, Products (8). |
| 240912-183844: | Class of Thursday September 12: Bases, Orders, Products (7). |
| 240912-183843: | Class of Thursday September 12: Bases, Orders, Products (6). |
| 240912-183842: | Class of Thursday September 12: Bases, Orders, Products (5). |
| 240912-183841: | Class of Thursday September 12: Bases, Orders, Products (4). |
| 240912-183840: | Class of Thursday September 12: Bases, Orders, Products (3). |
| 240912-183839: | Class of Thursday September 12: Bases, Orders, Products (2). |
| 240912-183838: | Class of Thursday September 12: Bases, Orders, Products. |
| 240910-175349: | Class of Tuesday September 10: Comparing topologies, bases for topologies (9). |
| 240910-175348: | Class of Tuesday September 10: Comparing topologies, bases for topologies (8). |
| 240910-175347: | Class of Tuesday September 10: Comparing topologies, bases for topologies (7). |
| 240910-175346: | Class of Tuesday September 10: Comparing topologies, bases for topologies (6). |
| 240910-175345: | Class of Tuesday September 10: Comparing topologies, bases for topologies (5). |
| 240910-175344: | Class of Tuesday September 10: Comparing topologies, bases for topologies (4). |
| 240910-175343: | Class of Tuesday September 10: Comparing topologies, bases for topologies (3). |
| 240910-175342: | Class of Tuesday September 10: Comparing topologies, bases for topologies (2). |
| 240910-175341: | Class of Tuesday September 10: Comparing topologies, bases for topologies. |
| 240905-163900: | Class of Thursday September 5: The definition of a topology (15). |
| 240905-163859: | Class of Thursday September 5: The definition of a topology (14). |
| 240905-163858: | Class of Thursday September 5: The definition of a topology (13). |
| 240905-163857: | Class of Thursday September 5: The definition of a topology (12). |
| 240905-163856: | Class of Thursday September 5: The definition of a topology (11). |
| 240905-163855: | Class of Thursday September 5: The definition of a topology (10). |
| 240905-163854: | Class of Thursday September 5: The definition of a topology (9). |
| 240905-163853: | Class of Thursday September 5: The definition of a topology (8). |
| 240905-163852: | Class of Thursday September 5: The definition of a topology (7). |
| 240905-163851: | Class of Thursday September 5: The definition of a topology (6). |
| 240905-163850: | Class of Thursday September 5: The definition of a topology (5). |
| 240905-163849: | Class of Thursday September 5: The definition of a topology (4). |
| 240905-163848: | Class of Thursday September 5: The definition of a topology (3). |
| 240905-163847: | Class of Thursday September 5: The definition of a topology (2). |
| 240905-163846: | Class of Thursday September 5: The definition of a topology. |
| 240903-162845: | Class of Tuesday September 3 (8). |
| 240903-162844: | Class of Tuesday September 3 (7). |
| 240903-162843: | Class of Tuesday September 3 (6). |
| 240903-162842: | Class of Tuesday September 3 (5). |
| 240903-162841: | Class of Tuesday September 3 (4). |
| 240903-162840: | Class of Tuesday September 3 (3). |
| 240903-162839: | Class of Tuesday September 3 (2). |
| 240903-162838: | Class of Tuesday September 3. |
| } |
Notes for BBS/24-327-241010-173951.jpg: [edit]